Transients(RC) elements in the circuit after commutation?

[gneill]

Is my result correct or not?


If it is sineware so I just need to find amplitude?
and U will be
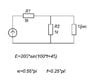
U=Umsin(wt+f)?

The instantaneous voltage on the capacitor will be a single, real value at some instant t. There will be no imaginary portion. Have you chosen a time t?

Yes, the voltage on the capacitor will be a sinewave of some amplitude. My calculation showed that there will be no phase angle associated with that sinewave; it has a form

U*sin(w*t)

where U is the amplitude.

The value that you proposed earlier, 72+69*j, is not the value I obtained for the voltage phasor on the capacitor. Perhaps you could check your calculation for the capacitor voltage.

 

[builder_user]

My I is 0.069+j*0.072.

What formula use to find shift between current and voltage?

 

[gneill]

My I is 0.069+j*0.072.

Which I would that be? The current supplied by E1? If so, it's not the value that I'm seeing.

 

[gneill]

My I is 0.069+j*0.072.

What formula use to find shift between current and voltage?

Find the angles of each and take the difference.

 

[builder_user]

Which I would that be? The current supplied by E1? If so, it's not the value that I'm seeing.

Hm..
My Req=(R2*1/j*w*C)/(R2+1/jwC)=998.8-35*j
Req2=R1+req=1998-35*j

E=200*(cos(45)+j*sin(45))=141.4+141.4*j

I=E/Req2

Circuit

 

[gneill]

The initial (pre-switching) circuit that you're analyzing is as depicted in the attached figure. You need to find Vc as a function of time. Then choose some time, t, at which the switch is thrown. The voltage on the capacitor at that instant of time is the voltage the capacitor will "take with it" to the new circuit configuration.

As you can see, in the figure, C1 and R2 are in parallel. You can determine an equivalent impedance for them. Call it Z1. R1 and Z1 form a voltage divider. So the output voltage will be E1 * (appropriate ratio involving R1 and Z1), where E1 is the phasor representing the source voltage.

 

[gneill]

Hm..
My Req=(R2*1/j*w*C)/(R2+1/jwC)=998.8-35*j
Req2=R1+req=1998-35*j

E=200*(cos(45)+j*sin(45))=141.4+141.4*j

I agree with your E.

Something's funny with your Req. What value are you using for w? What value do you have for 1/jwC ?

 

[gneill]

I see from your figure in post #35 that you've assumed that 100*t implies 100 degrees per second for the angular frequency. I've been assuming that it's 100 radians per second.

This makes a big difference! (Like all the nice round numbers that I've been seeing will go away! -- including a particularly trivial value for the voltage on the capacitor at time t = 0!).

Do you stick to the 100 degrees per second choice?

 

[builder_user]

1/0.56*3.14*j*20^-6

 

[builder_user]

I see from your figure in post #35 that you've assumed that 100*t implies 100 degrees per second for the angular frequency. I've been assuming that it's 100 radians per second.

This makes a big difference! (Like all the nice round numbers that I've been seeing will go away! -- including a particularly trivial value for the voltage on the capacitor at time t = 0!).

Do you stick to the 100 degrees per second choice?

Yes of course 'cause we always use degrees.

 

[gneill]

Yes of course 'cause we always use degrees.

Okay, give me a moment to make the changes in my figures.

 

[gneill]

C1 || R2 ==> 998.8 - 34.86j Ω

Vc ==> 71.92 + 69.45j V or, 100V @ 44°

I ==> 0.069 + 0.072j A or, 0.10A @ 46°

Does that correspond to what you're seeing?

 

[builder_user]

C1 || R2 ==> 998.8 - 34.86j Ω

Vc ==> 71.92 + 69.45j V or, 100V @ 44°

I ==> 0.069 + 0.072j A or, 0.10A @ 46°

Does that correspond to what you're seeing?

Yes it does

 

[gneill]

Okay. Have you chosen a time t for when the switch is to be thrown?

 

[builder_user]

Okay. Have you chosen a time t for when the switch is to be thrown?

I can make choice?I know only t=0 and t!=0.that's all that I know about time

 

[gneill]

I have a choice?I know only t=0 and t!=0.that's all that I know about time

The voltage on the capacitor, before the switch is thrown, is a sine wave -- it changes with time. So the value of the voltage at any given time depends upon, well, the time!

So you can get any value up to and including +/- the magnitude of that sine wave on the capacitor depending upon what time you choose to throw the switch.

If you choose time t = 0, then you'll have to calculate the value of the sinewave for that time.



Just as a note for interest, when I was using 100 rad/sec as the angular frequency, the phase shift built into the source voltage was canceled by the RC network, and the voltage across the capacitor became a sinewave with no phase shift. So the voltage on the capacitor at time t = 0 was zero! Very easy to find the solution after the switch was thrown in that case!

 

[builder_user]

So I need to use t=0?And u(0)=0?

Before commutation t=0 so U(o)=0
After commutation it will be simple circuit with DC and two resistors?

And dif.equatations will be the same as in previous case right?

 

[gneill]

So I need to use t=0?And u(0)=0?

Before commutation t=0 so U(o)=0
After commutation it will be simple circuit with DC and two resistors?

And dif.equatations will be the same as in previous case right?

U(0) will not be zero. Remember, there is a phase associated with the supply voltage, and another phase associated with the capacitor voltage. When t=0, the phase of the capacitor voltage will be the argument of sine function for the voltage on the capacitor.

After commutation, yes, the circuit will be a DC one as you say, with DC voltage E2 and whatever voltage you have found already on the capacitor.

 

[builder_user]

U(0) will not be zero. Remember, there is a phase associated with the supply voltage, and another phase associated with the capacitor voltage. When t=0, the phase of the capacitor voltage will be the argument of sine function for the voltage on the capacitor.

But if U=Umsin(w*t) t=0->sin(0)=0 and U=0

 

[gneill]

What result did you obtain for the voltage on the capacitor as a function of time? Didn't the phasor result have a angle?

 

[builder_user]

Аh! I see.

Didn't the phasor result have a angle?

I forgot formula for amplitude. arcsin(x)=f <- phase

 

[gneill]

For x = a + jb, amplitude is sqrt(a² + b²). The phase angle is atan(b/a), but beware of the quadrant... the trig functions on a calculator deal with "priciple values" over a limited domain. If using MathCad, the atan2 function is available. Or, if you're working directly with complex numbers, |x| is the amplitude and arg(x) will give the correct angle.

 

[builder_user]

U=100*(0.72+j*0.69)

f=arcsin(0.72)=arcos(0.69)=46*

so for t=0
U=100*sin(0+46)=72?

 

[gneill]

atan(0.69/0.72) = 43.8°

I calculated 44° ...

 

[builder_user]

Oh.
43.9=44*

я used arcsin(0.72) but sin(x)=0.69 so arcsin(0.69) is needed

 

[builder_user]

last question.
How this circuit looks before & after commutation?
Is my circuits correct?

 

[gneill]

In the 'after commutation' circuit, immediately after the switch opens the capacitor will have a voltage on it that will want to discharge through the resistors R3 and R4. After a long time, the capacitor should look like an open circuit, not a short circuit.

 

[builder_user]

In the 'after commutation' circuit, immediately after the switch opens the capacitor will have a voltage on it that will want to discharge through the resistors R3 and R4. After a long time, the capacitor should look like an open circuit, not a sort circuit.

This circuits?

Long time after commutation I only need to find voltage on R3?Is R4 in the circuit?

Immediately after commutation I need to find current on resistor R4?

 

[gneill]

The circuit on the left looks fine for a long time after commutation. Note that there will be no current through R4.

For the circuit on the right, representing the instant immediately after commutation, if the capacitor had zero voltage on it from before, then the circuit is correct.

 

[builder_user]

The circuit on the left looks fine for a long time after commutation. Note that there will be no current through R4.

For the circuit on the right, representing the instant immediately after commutation, if the capacitor had zero voltage on it from before, then the circuit is correct.

Really?Great!
But if before commutation Uc was !=0 so It would look like long time or not?