Transition Matrices - Worded Problem

[mathsashelp]

A very small country town has a population that can be grouped according to three categories: adults teenagers and children.

Each year statistics show that:

Children are born at the rate of 4% of the adult population 12% of children become teenagers 15% of teenagers become adults 0.5% of children die 3% of teenagers die 8% of adults die

Presuming that the town started with 350 children, 640 teenagers and 2100 adults, find how many there will be of each category after 10 years.

I'm having trouble finding the transition matrix.

So far I've got.
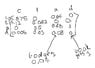
c t a d
c [0.875 0 0.04 0]
t [ 0.12 0.082 0 0]
a [ 0 0.15 0,88 0]
d [ 0.005 0.03 0.08 0]

The textbook somehow gets 0.04 in the 4th row of the 3rd column instead of 0.08 and has a 1 in the 4th row of the 4th column instead of 0.

Not sure how or why.

If I could get the Transition matrix correct I understand that it would simply be

T^10 x initial state but I'm just having trouble setting it out.

Thanks

 

[BvU]

Hello math, welcome to PF !

$$\begin{bmatrix} c', t', a', d'
\end{bmatrix} =

\begin{bmatrix}0.875 & 0.000 & 0.040 & 0 \\
0.120 & 0.082 & 0.000 & 0 \\
0.000 & 0.150 & 0.880 & 0 \\
0.005 & 0.030 & 0.080 & 0 \\
\end{bmatrix}
\begin{bmatrix} c \\ t \\ a \\ d \\ \end{bmatrix}
$$is the general idea, I hope, where the accents denote a shift by 1 year.

All columns add up to 1, except 2 and 4 in your rendering of the matrix. Whereas the book probably only has column 3 not adding up to 1,
so it looks like an error in the book to me. The 0.04 I can't explain either.
Like your 0.082 seems an error by you...

Funny it's a 4x4 matrix when you only have three categories and the last column is all zeroes.

The book doesn't have that, which indicates to me that once you're dead, you remain dead.
But again, that category isn't counted, so I wouldn't worry.

If still in doubt, let your matrix^10 loose and see if the results are credible !

Isn't it nice to see such a cute society develop: no teenage pregnancies !

 

[haruspex]

I agree with your .08. For the [d,d] position, dead people stay dead.
How do you get the 0.88? The 0.082 should be 0.82.

 

[BvU]

Very good Haru ! Makes me recall the stuff about columns adding up to 1: a category like a can have > 1 because it really the 4% that become parent remain a