charlie05
- 128
- 6
Homework Statement
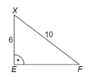
Points E and F are the focuses of the hyperbola and point X are on the hyperbola. Determine the size of the main and minor half-axes of the hyperbola.
Homework Equations
x2 = e2 - f2
x = 8
The Attempt at a Solution
I think that eccentricity is 4 units (x/2). But I don’t know how to continue.