Triangle inside circle, find area of circle.

[Feodalherren]

Homework Statement

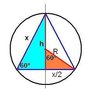
An equilateral triangle of side x is is inscribed in a circle. Express the area of the circle as a function of x.

Homework Equations

Anything non-trig. I suspect it's got something to do with the Pythagorean theorem.

The Attempt at a Solution

I tried getting the radius of the circle by taking ((1/2)x)^2 + y^2 = r^2

My y value was in terms of x. I ended up with an equation that looked nothing like the answer which is supposed to be A(x)=(∏/3)x^2

I what I don't see is how I can get r in terms of x to make any sense.

 

[ehild]

You need a drawing first, like the one attached. You see two similar right triangles. Do you know how the height h is related to the side length of an equilateral triangle?

ehild

 

[Feodalherren]

First off, thank you very much for such a quick response. Yes. I have made this sketch but it hasn't been of much help yet. I know that the relation is ((1/2)x)^2+something^2=r^2

What I don't understand is how the h would be of any help? It is not the full diameter...

 

[Saitama]

What I don't understand is how the h would be of any help? It is not the full diameter...

Use Pythagoras Theorem to find h. Consider the blue triangle in ehild's sketch. You have the hypotenuse and one side. You can find the second side i.e. h using Pythagoras theorem.

 

[Feodalherren]

You mean to find the entire h? That's the problem. I can easily see that I can get h in terms of x. The problem is that I don't see how h would be of any use to me.

 

[Saitama]

You mean to find the entire h? That's the problem. I can easily see that I can get h in terms of x. The problem is that I don't see how h would be of any use to me.

Sorry i misread your question.

Aren't you allowed to use trig? It can be easily solved by using trig.

 

[Curious3141]

You mean to find the entire h? That's the problem. I can easily see that I can get h in terms of x. The problem is that I don't see how h would be of any use to me.

Once you get h, you can make use of a well-known geometric property that the perpendicular bisectors of the sides of an equilateral triangle divide each other in a ratio of 2:1. With that, you can immediately work out the radius of the circle.

 

[Feodalherren]

No. I haven't done trig yet.

 

[Feodalherren]

Once you get h, you can make use of a well-known geometric property that the perpendicular bisectors of the sides of an equilateral triangle divide each other in a ratio of 2:1. With that, you can immediately work out the radius of the circle.

Can you explain please? That made no sense to me :(.

 

[Saitama]

Once you get h, you can make use of a well-known geometric property that the perpendicular bisectors of the sides of an equilateral triangle divide each other in a ratio of 2:1. With that, you can immediately work out the radius of the circle.

Or rather, you can use a dirty method too...
Find h. In the red triangle find the second side which would be:
\sqrt{R^2-\frac{x^2}{4}}
h-\sqrt{R^2-\frac{x^2}{4}}=R

Solve this equation to get R. Substitute the value h. You will need to square both the sides to get R.

 

[Curious3141]

Can you explain please? That made no sense to me :(.

Well, it's a property of ALL triangles, really. The bisector of a side, when produced to the opposite vertex, is called a median. There are 3 medians, and they all intersect at one point called the centroid. The centroid always divides each median in the ratio 2:1. So the short length is 1/3 of the median, the long one is 2/3.

You can see the diagram and read more here: http://en.wikipedia.org/wiki/Median_(geometry )

Of course, in an equilateral triangle, the symmetry is perfect, and the bisectors of each side are also perpendicular bisectors. The median of the equilateral triangle is of length h. By symmetry, the centroid of the triangle coincides with the centre of the circle. So what's the radius of the circle?

 

[ehild]

From Pythagoras theorem. h=√3/2 x. x and h in the big triangle corresponds to R and x/2 in the small triangle. The coloured triangles are similar, the ratios of the corresponding sides are the same. Write up this equation. You can find the radius of the circle from that.

ehild

 

[Feodalherren]

I must be retarded... I don' get it. I tried getting the h of the small triangle, like you did. I called the h of the small triangle y and this is what I did.

y=\sqrt{}(x^2/4+r^2)

at this point let y = \sqrt{}b to save me from writing it all over again.

r^2=\sqrt{}(b)^2 + (\frac{}{}x^2/2)^2

r=\sqrt{}(b+((x^2)/4)Area = ∏\left(\sqrt{}(b+((x^2)/4)\right)^2

Fully simplified

A=\pi\left((2/4)x^2 + r^2\right)

 

[Saitama]

I must be retarded... I don' get it. I tried getting the h of the small triangle, like you did. I called the h of the small triangle y and this is what I did.

y=\sqrt{(x^2/4+r^2)}

Assuming that r is radius, the equation is wrong. The correct equation is this:
y=\sqrt{r^2-\frac{x^2}{4}}

Try to understand what Curious said, that's much simpler.

 

[Feodalherren]

Ok screw this. I'm scanning in my notes. I can't deal with this thing. Give me a minute.

I know I missed a minus sign when I swapped the y term over but it still comes out wrong. It's problem 43.

 

[Curious3141]

Try to understand what Curious said, that's much simpler.

Thank you, yes, this method is really simple. In fact, I was able to work the whole thing out in my head. Why take the complicated approach?

 

[ehild]

You do not need y. But you must to know that h=√3/2 x.

From the similarity of the shaded triangles, x:h=R:(x/2), that is Rh=x²/2.

Or you apply what Curious said, R=2/3 h.

ehild

 

[Saitama]

Thank you, yes, this method is really simple. In fact, I was able to work the whole thing out in my head. Why take the complicated approach?

Yep, that 2:1 ratio did not strike my mind at the first sight.

 

[Feodalherren]

I would love to do as you said but honestly I can't. I need somebody to show me.

 

[Saitama]

I would love to do as you said but honestly I can't. I need somebody to show me.

Assuming that you know what a centroid and median is, there's a property which is already mentioned by Curious.
The centroid cuts every median in the ratio 2:1, i.e. the distance between a vertex and the centroid is twice as long as the distance between the centroid and the midpoint of the opposite side.

If you see the question, you notice that the radius of circle is 2/3 of the height of the triangle using the above mentioned property. I guess you know how to work with the ratios.

 

[Feodalherren]

No I don't and I've never heard anything about a centroid. I give up. You can't teach an idiot to do math. I'm going to bed and I'm getting a B.

I appreciate all the effort to help but it looks like I'm just a retard.

 

[Saitama]

No I don't and I've never heard anything about a centroid. I give up. You can't teach an idiot to do math. I'm going to bed and I'm getting a B.

Similar triangles?

 

[Farvahar]

Well you could simply do this:
If the side of the triangle is X then you can simply calculate the R that collides with the head of one of the sides and since the perpendicular line from O to that side would divide it to 2 halves:
R=X/2sin60° and its solved. I'm not familiar with US education so may I ask what grade was this question for?