Taylor_1989
- 400
- 14
I am having trouble figuring out these two word problems. I have attached drawing on how I have set them up the diagrams up, but I seem to be going wrong on both. Here are the two questions.
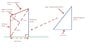
1. A rocket lifts off vertically and travels to height of 5000m. The second stage cuts in and takes the rocket at an angle of 25 degrees, to the vertical, covering a further distance of 2000m. Calculate the height of the rocket.
2. An aeroplane is apporaching an airport at a height of 1000 m. If the aeroplane is 8km from the airport, workout the angle of approach.
The dotted line in diagrams show my working method.
If someone could please show me where I am going wrong, on these diagrams, I would appreciate very much.
In the first diagram I got 155 degree from take 180 - 25
1. A rocket lifts off vertically and travels to height of 5000m. The second stage cuts in and takes the rocket at an angle of 25 degrees, to the vertical, covering a further distance of 2000m. Calculate the height of the rocket.
2. An aeroplane is apporaching an airport at a height of 1000 m. If the aeroplane is 8km from the airport, workout the angle of approach.
The dotted line in diagrams show my working method.
If someone could please show me where I am going wrong, on these diagrams, I would appreciate very much.
In the first diagram I got 155 degree from take 180 - 25