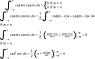Emphacy
- 3
- 0
Hello everyone, I've wandered PF a few times in the past but never thought I'd join, here I am, how exciting.
To keep it short I'm trying to understand the proof behind Fourier Series and can't quite get to grips with basic trigonometric orthogonality.
I understand that sin and cos are naturally orthogonal but I'm having difficulty understanding this:
<br /> \int_{-\pi}^{\pi}\cos(mx)\cos(nx)\, dx=\pi\delta_{mn} \,\,\,where\,\delta_{mn}=\begin{cases} <br /> &\text{1 if } m=n \\ <br /> &\text{0 if } m\neq n <br /> \end{cases}<br />
It makes sense that the area is \pi if m=n because you get this waveform and zero if m is an integer multiple of n because you get this waveform (here the negative areas cancel the positive areas from -\pi to \pi)
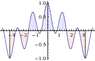
BUT... If m\neq n AND is sufficiently close e.g (m=2, n=2.1) you get this waveform, in which case the area from -\pi to \pi is clearly not zero.
What gives? Does this only apply if m and n are different by integer multiples?
Thanks for your time! (:
To keep it short I'm trying to understand the proof behind Fourier Series and can't quite get to grips with basic trigonometric orthogonality.
I understand that sin and cos are naturally orthogonal but I'm having difficulty understanding this:
<br /> \int_{-\pi}^{\pi}\cos(mx)\cos(nx)\, dx=\pi\delta_{mn} \,\,\,where\,\delta_{mn}=\begin{cases} <br /> &\text{1 if } m=n \\ <br /> &\text{0 if } m\neq n <br /> \end{cases}<br />
It makes sense that the area is \pi if m=n because you get this waveform and zero if m is an integer multiple of n because you get this waveform (here the negative areas cancel the positive areas from -\pi to \pi)
BUT... If m\neq n AND is sufficiently close e.g (m=2, n=2.1) you get this waveform, in which case the area from -\pi to \pi is clearly not zero.
What gives? Does this only apply if m and n are different by integer multiples?
Thanks for your time! (:
Last edited: