Nexor
- 12
- 0
Cheating in the game :)
I play this game, Minecraft, and I have to find a place called stronghold, which can only be found by throwing "eye of enders" in the air, that go in the direction of where the stronghold is hidden. The only problem is, those eyes are very rare and difficult to get, so I thought something about this: by throwing only 2 ender eyes, I can get the coordinates of the stronghold. The picture might be more understandable. You guys think this can be done by using trigonometry? What formula should I use?? :)
Thanks in advance,
Nexor.
EDIT: x3,y3 would be the stronghold's location. :)
I play this game, Minecraft, and I have to find a place called stronghold, which can only be found by throwing "eye of enders" in the air, that go in the direction of where the stronghold is hidden. The only problem is, those eyes are very rare and difficult to get, so I thought something about this: by throwing only 2 ender eyes, I can get the coordinates of the stronghold. The picture might be more understandable. You guys think this can be done by using trigonometry? What formula should I use?? :)
Thanks in advance,
Nexor.
EDIT: x3,y3 would be the stronghold's location. :)
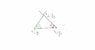
 D
D