Jemal
- 8
- 0
Triple battery Circuit? (Kirchoff help)
Hey guys I really just don't know how to solve this...
Can anyone help me? Like just give me some guidelines on how exactly kirchhoffs laws work and how i can use them on this problem?
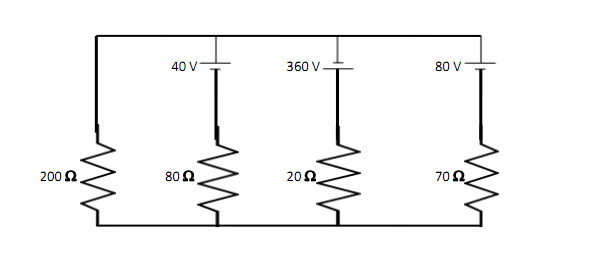
I need to find the values and directions of the currents in each branch.
Hey guys I really just don't know how to solve this...
Can anyone help me? Like just give me some guidelines on how exactly kirchhoffs laws work and how i can use them on this problem?
I need to find the values and directions of the currents in each branch.