Triple Integral Limits Setup Cartesian

[paul2211]

Homework Statement

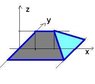
Find volume bounded by: $x - z = 0; x + z = 3; y + z = 1; z = y + 1; z = 0$

Homework Equations

Vol = $\int\int\int_{V}dV$

The Attempt at a Solution

I really don't know how to begin this problem because I have trouble visualizing what all those intersection of planes will look like. Usually if it's 2 surfaces, I can see it no problem.

Do you guys have some systematic way to find the limits for volumes using triple integrals? My prof isn't the best since we didn't even get to line integrals and etc for our Multivariable Calc class...

 

[ehild]

Find the points where three planes intersect. What shape do you get?
Imagine that you cut this shape parallel with the (x,y) plane at different heights z=h. How the cross-sections look like?
I attach a figure that might help to imagine the shape. ehild

 

[HallsofIvy]

The first thing you should do is draw a graph. Because it is difficult to draw in three dimensions, I prefer to draw xy, xz, and yz graphs. Here, none of the equations involve both x and y so you really only need xz and yz graphs.

x- z= 0 is the z= x line, of course, and x+ z= 3 is the line z= 3- x that has x intercept (0, 3) and z intercept (3, 0). Draw those two lines on the xz-graph.

y+ z= 1 is the line z= 1- y with y intercept (1, 0) and z intercept (0, 1). z= y+ 1 has y intercept (-1, 0) and z intercept (0, 1). Draw those two lines.

Now, imagine turning the yz graph so its z axis corresponds to the z axis on the xz graph. That will give you some idea of what the figure looks like. Now, looking at that, there is nothing bounding the region between z= 1- y and z= y+ 1 in the y-direction. Adding the "z= 0" condition we do have a bounded region below the z= 1- y plane but then the z= y+ 1 plane plays no part. The only bounded region I see here lies within the triangle bounded by z= x, z= 3- x, and z= 0 below the plane z= y+ 1.

I see that, for that region, x lies between 0 and 1. For each x, z lies below the two lines x- z= 0 and x+ z= 3. I think, then that we will need to break this into two integrals, the first for x= 0 to the x-coordinate of the point of intersection, the second for x= that value to 3.

 

[ehild]

To find the integration limits, it is useful to plot contours of equal height (equal z) together with the projections onto the (x,z) and (yz) planes, HallsofIvy suggested.

x - z = 0; x + z = 3; y + z = 1; z = y + 1; z = 0.

For a given z=a>0, the equations yield the following contour lines:

x=a, x=3-a, y=1-a, y=-(1-a).

See attached picture. It shows the contours of equal z on the (x,y ) plane, together with the projections of the shape onto the (x,z) and (y,z) planes. The shape is like a roof, as shown in my previous post.
It is easy to find out the integration limits from the plots now:

0<x<3, -(1-z)<y<1-z

The y-z lines intersect at the point y=0, z=1, so the volume is between z=0 and z=1.

0<z<1.

ehild