ERoday
- 3
- 0
This a book example that I have the answer to but do not understand.
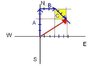
What are the magnitude and direction of the total displacement for the treasure hunt? The instructions to find the treasure are 5 paces North, 3 paces East, then 4 paces Southeast. Each pace is 0.750 m in length.
So I understand that to find the total displacement you need to find the components of each vector. So 5 pace North = vector [A] which would be Ax= 0 and Ay= 3.75m, and 3 paces east =vector which would be Bx= 2.25m and By= 0 but for 4 paces southeast the book gives the answer to be Cx=2.12 and Cy =-2.12 and I understand why those components are positive and negative but not why the distance is 2.12. Why isn't it Cx=3.00m and Cy= -3.00m?
What are the magnitude and direction of the total displacement for the treasure hunt? The instructions to find the treasure are 5 paces North, 3 paces East, then 4 paces Southeast. Each pace is 0.750 m in length.
So I understand that to find the total displacement you need to find the components of each vector. So 5 pace North = vector [A] which would be Ax= 0 and Ay= 3.75m, and 3 paces east =vector which would be Bx= 2.25m and By= 0 but for 4 paces southeast the book gives the answer to be Cx=2.12 and Cy =-2.12 and I understand why those components are positive and negative but not why the distance is 2.12. Why isn't it Cx=3.00m and Cy= -3.00m?