navm1
- 44
- 0
Homework Statement
Got my first physics assignment and I've been able to work out (I think) all of them except these two.
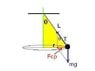
1. A conical pendulum has length 1.5m and rotates at 4ms^-1. What is its angle to the vertical?
2. A mass moves in a vertical circle attached to a fixed point by a string of length 2m. How fast must it be moving at the lowest point if it completes circles? What would be the speed necessary at the lowest point if the mass were attached by a light rod instead of a string?
Homework Equations
F=ma
F=mv^2/r
v=rω
ω=θ/r
The Attempt at a Solution
1. I've drawn a diagram and understand that i have gravity acting downwards and tension up the string. I think i could find θ by using tanθ=v^2/rg but I am not sure of how to work the radius out if i only have the length of the string, the velocity, and gravity.
2.
I'm only given the length and gravity on this question. I think i might have to work out the tension but I am finding it difficult without knowing a mass of the object.
I understand my attempts didn't go too far. Tension, work, and energy were omitted from my course for some reason so I've got some catching up to do with it. Thanks