David Mordigal
- 6
- 0
This is a problem from my physics homework. I copied the diagram below as best I could from the text. It's not the best rendering but you'll get the idea.
1. Homework Statement
Two blocks are at rest on a frictionless incline, as shown in the figure.
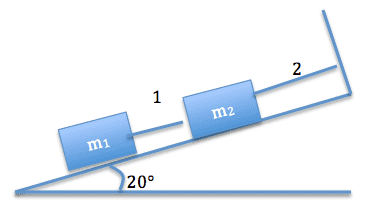
Part A. What is the tension in the string number 1 if m1 = 9.0kg and m2 = 3.9kg?
Part B. What is the tension in the string number 2 if m1 = 9.0kg and m2 = 3.9kg?
The answer to Part A is: T1 = 30.2 N, which I don't understand.
So far, I know the following:
F = ma
Fx = max
Fy = may
w = wy = mg = 9.0kg * 9.8 m/s2 = 88.2 N
I tried splitting the tension of string 1 into its vector x and y components, but that wasn't getting me to the right answer. I am not quite sure where to start or how they got that answer, 30.2 N (part A). Any guidance would be much appreciated.
Ty = mg = 88.2 N
T = Ty/sin(20) = 257.9 N
1. Homework Statement
Two blocks are at rest on a frictionless incline, as shown in the figure.
Part A. What is the tension in the string number 1 if m1 = 9.0kg and m2 = 3.9kg?
Part B. What is the tension in the string number 2 if m1 = 9.0kg and m2 = 3.9kg?
The answer to Part A is: T1 = 30.2 N, which I don't understand.
Homework Equations
So far, I know the following:
F = ma
Fx = max
Fy = may
w = wy = mg = 9.0kg * 9.8 m/s2 = 88.2 N
The Attempt at a Solution
I tried splitting the tension of string 1 into its vector x and y components, but that wasn't getting me to the right answer. I am not quite sure where to start or how they got that answer, 30.2 N (part A). Any guidance would be much appreciated.
Ty = mg = 88.2 N
T = Ty/sin(20) = 257.9 N