Two moving blocks, find small blocks final velocity

[toastie]

Homework Statement

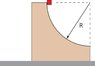
A small block (mass m) slides down a circular path (radius R) which is cut into a large block (mass M), as shown. M rests on a table and both blocks slide without friction. The blocks are initially at rest, and m starts at the top of the path. Determine the velocity of m when it loses contact with the large block.
Data: M = 3.4 kg; m = 1.2 kg; R = 0.7 m.

Homework Equations

Using basic geometry I have solved a = (angular velocity^2)*r*cos(phi)cos(theta)

The Attempt at a Solution

Using the above equation though, I believe to be in the wrong refrence frame since both blocks are moving. Thus, the 90 degree refrence angles will not be 90 when the small block is no longer touching the large block.

Thank you in advance!

 

[LowlyPion]

Maybe consider the energy that's in the system?

Don't you have a total of m*g*R available?

And won't the Center of Mass in the absence of external forces need to be in the same position when the small block exits?