- #1
mikeph
- 1,235
- 18
Hi
I have two images and I want to compare the "structures" of them at different scales. I remember from cosmology that the two point correlation function was used to extract similar structural information from the CMB, generating a graph of structure Vs scale. Then at certain length scales you have peaks which correspond to physical occurrences.
edit-this is the image I'm talking about.
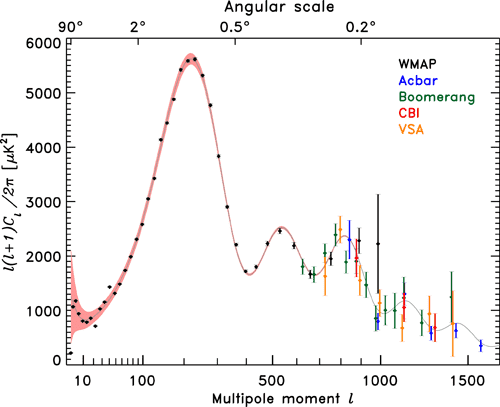 This is exactly what I'd like to apply to my image, but after searching the internet I can't find much that helps me actually numerically calculate this for an image. Does anyone know any good tutorials for actually doing this?It's my understanding that this method is favourable to taking a Fourier/cosine transform as these methods are biased towards finding structure along the x-y axes? My image is isotropic so I have no reason to care about one direction more than another.
This is exactly what I'd like to apply to my image, but after searching the internet I can't find much that helps me actually numerically calculate this for an image. Does anyone know any good tutorials for actually doing this?It's my understanding that this method is favourable to taking a Fourier/cosine transform as these methods are biased towards finding structure along the x-y axes? My image is isotropic so I have no reason to care about one direction more than another.
Any help or pointing me in the right direction would be brilliant, thanks
Mike
I have two images and I want to compare the "structures" of them at different scales. I remember from cosmology that the two point correlation function was used to extract similar structural information from the CMB, generating a graph of structure Vs scale. Then at certain length scales you have peaks which correspond to physical occurrences.
edit-this is the image I'm talking about.
Any help or pointing me in the right direction would be brilliant, thanks
Mike