Two Stage Epicyclic Gear-box - Finding the Gear ratio

[Master1022]

Homework Statement

Find the gear ratio when Brake 1 is applied, the clutch is disengaged and Brake 2 is
released.

Relevant Equations

$$\frac{\omega_1}{\omega_2} = \frac{r_2}{r_1} = \frac{N_2}{N_1}$$

Hi,

Just have a question about the method in attempting this two-stage epicyclic gear-box.

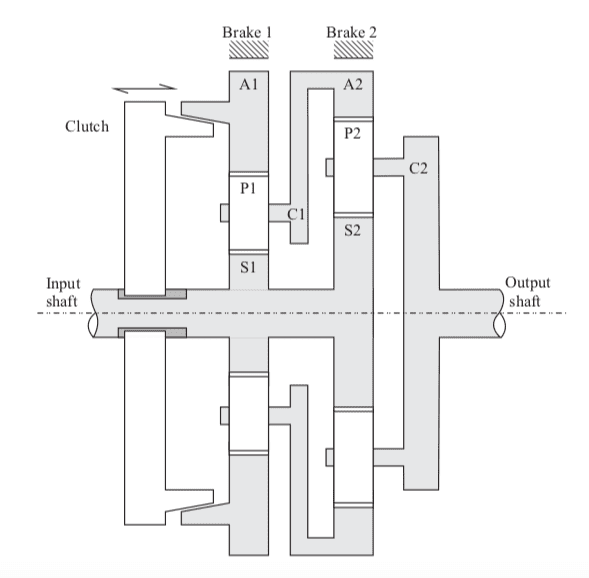
We are given the following information about the number of teeth: S1 = 48, P1 = 28, S2 = 96, and P2 = 48

My attempt:
1. Work out the number of teeth for the two ring/annulus gears
From geometry, we can find that A1 = 104, A2 = 192

2. Find the ratio between the input and output (gear ratio)
So the input is $\omega_{S_1} = \omega_{S_2} = \omega_{in}$ and $\omega_{out} = \omega_{S_2}$

Then I will start the method of considering motion with the carrier and then relative to the carrier

- I considered everything relative to C2

Here is where I went wrong and I am looking for the reason why:
- Then we know that the total $\omega_{A1} = 0$ as brake 1 is applied, thus I set the motion of A1 relative to C2 as $-\omega_{C_2}$ (so that it sums to 0)
Why was it wrong for me to consider both stages at once (i.e. by relating C2 and A1 directly as I have done)?
- From there, I just used the gear equations to get that $\omega_{S} = \omega_{C_2} \left( 1 + \frac{N_{A_1}}{N_{S_1}} \right)$. From there we can simply divide out the speed of the carrier (output) and get the gear ratio.

The solution considered the whole gearbox in two stages and did:
(overview: set up some simultaneous equations and solve for unknowns)
1. Consider speed of second stage relative to C2
2. Set an arbitrary speed of A2 relative to C2 (we now have a total of $\omega_{C_2} + \omega_{Q}$)
3. Now consider the first stage of the gearbox (the speed of C1 is the same as A2)
4. Now we can use the A1 has no speed condition to get relative speed of A1
5. Then we can get relative and total speeds of P1 and S1
(now we have an equation for S1 in terms of $\omega_{C_2}$ and $\omega_{Q}$)
6. To find $\omega_{Q}$, we once again consider the second stage of the gearbox and use relative motion of A2 to work our way down to an equation for S2 in terms of $\omega_{C_2}$ and $\omega_{Q}$
7. Set S1 = S2 and solve for $\omega_{Q}$ in terms of $\omega_{C_2}$
8. Substitute it back in get our ratio.

So I understand this method, but am wondering why I cannot directly consider speed of A1 relative to C2?

I realize that I have mainly provided a qualitative description of the method, but I don't really know how to write it out as the method just involves filling in tables - I will provide any clarification that is required,

Thanks in advance

 

[anothermike]

Are you still seeking an answer for this? I see that it was posted some weeks ago.

 

[anothermike]

I worked this out from first principles and came up with ω_out = $\frac{31}{57}$ω_in.

Your mistake was in the assumption that ω_out = ω_S2. The annular gear A2 is turning as a result of the movement from the first stage, and so C2 will have a movement that is determined from both S2 and A2 through P2. To solve the problem, I found it easier to consider linear speeds rather than angular speeds, and then divide out the final radius at the end to get the final ω_out.

So plate C1 is moving at a linear speed (at the points where it connects to the axles of P1) that is halfway between the at-rest A1 and the turning S1, with the P1 spinning between them. The resulting ω_C1 (which does equal ω_A2 as you indicated), is that linear speed divided by the radius at the axis of P1. That gives us ω_A2 = $\frac{24}{76}$ω_in. We then have C2 at the axle of the P2 gears moving at a linear speed that is halfway between 96ω_in, from S2, and 192ω_A2, from A2. Dividing that result by the radius of 144 at the P2 axle for C2 yields the ω_out that I calculated above.

Hope this helps!

 

[Master1022]

@anothermike - thank you so much for taking the time to reply and help me out! I apologise for not responding for so long, but I have taken such a long break from the subject (so I just started remembering the concepts now whilst getting back into it).

I worked this out from first principles and came up with ω_out = $\frac{31}{57}$ω_in.

Your mistake was in the assumption that ω_out = ω_S2.

Yes, that is true, I am not sure why I thought that.

The annular gear A2 is turning as a result of the movement from the first stage, and so C2 will have a movement that is determined from both S2 and A2 through P2. To solve the problem, I found it easier to consider linear speeds rather than angular speeds, and then divide out the final radius at the end to get the final ω_out.

Just want to confirm, but is the carrier velocity (when in the standard epicyclic gear train) always the average of the two surrounding velocities? This makes sense intuitively as the velocity should vary linearly across the planetary gear.

So plate C1 is moving at a linear speed (at the points where it connects to the axles of P1) that is halfway between the at-rest A1 and the turning S1, with the P1 spinning between them. The resulting ω_C1 (which does equal ω_A2 as you indicated), is that linear speed divided by the radius at the axis of P1. That gives us ω_A2 = $\frac{24}{76}$ω_in. We then have C2 at the axle of the P2 gears moving at a linear speed that is halfway between 96ω_in, from S2, and 192ω_A2, from A2. Dividing that result by the radius of 144 at the P2 axle for C2 yields the ω_out that I calculated above.

Hope this helps!

Yes, thank you very much! Your method is so much faster than mine - I hadn't ever thought about it this way! I will be sure to use this method going forward.

In case anyone else reads this, I did retry the problem and use a tabular method twice. Once was considering all of the '1' gears relative to C1. That yielded an expression for $\omega_{S_1} = f(\omega_{C_1})$. Then I used a second tabular method to analyse the '2' gears relative to C2 - an extra variable needs to be introduced in this part to form a system of equations. You can then get an algebraic solution from there which yields the same answer as @anothermike 's post. However, @anothermike 's method is so much simpler.

 

[Master1022]

Your mistake was in the assumption that ω_out = ω_S2. The annular gear A2 is turning as a result of the movement from the first stage, and so C2 will have a movement that is determined from both S2 and A2 through P2. To solve the problem, I found it easier to consider linear speeds rather than angular speeds, and then divide out the final radius at the end to get the final ω_out.

I think I have seen a method similar to this before (i.e. where we consider velocity profiles). Is this method only applicable in situations where there is a ring gear present? For example, I have seen some problems where there is just a sun gear and a planet gear and was unable to see how this method could be applied.

 

[anothermike]

Just want to confirm, but is the carrier velocity (when in the standard epicyclic gear train) always the average of the two surrounding velocities? This makes sense intuitively as the velocity should vary linearly across the planetary gear.

Yes, it is. If you think about it, the rim of the carrier gear is traveling with a constant speed relative to its axis, and where it makes contact with the other surrounding gears, one velocity is $v_c + \omega r$, and the other is $v_c - \omega r$. It thereby follows that $v_c$ would be the average of the two.

 

[anothermike]

I think I have seen a method similar to this before (i.e. where we consider velocity profiles). Is this method only applicable in situations where there is a ring gear present? For example, I have seen some problems where there is just a sun gear and a planet gear and was unable to see how this method could be applied.

I believe this method would be applicable in all situations, though perhaps unnecessary. If you post one of those sun gear and planet gear problems, I'll take a look and see if I can apply it.