Uncertainty in the intersection of two lines with error bars

[SuchBants]

The only thing I wish to take from this graph is the intersect of the two lines of best fit. How can I get the uncertainty in this point?
While the points appear to have the same uncertainties, they actually each have their own distinct % uncertainty.

Would the maximum uncertainty in the X value of the intersect be the uncertainty of the largest error bar in the x direction? And similarly for the y value?

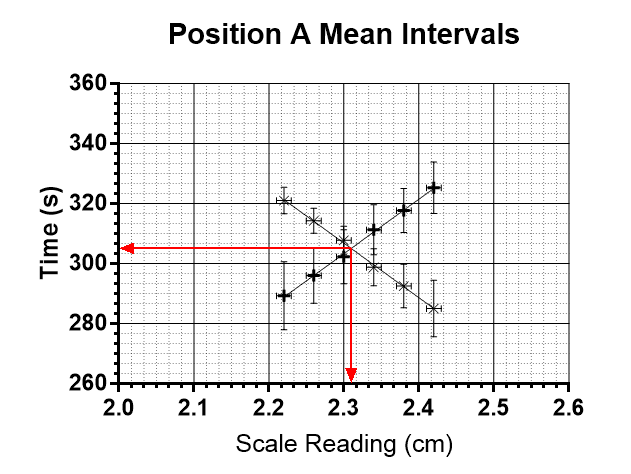
Here is an image of the graph

 

[kuruman]

Can you not do standard error propagation using the slope and intercept uncertainties?

 

[SuchBants]

Can you not do standard error propagation using the slope and intercept uncertainties?

I have 0 idea what that means.

 

[kuruman]

How did you get the straight lines that you show in the figure? If you used some type of canned linear regression program, the uncertainties in the slopes should be available. In fact, as I look at your figure, there is no scatter in your data points. Why are your error bars so large?

What I mean is that if the straight lines are characterized by y = a₁x + b₁ and y = a₂x + b₂, then you should have an idea of the uncertainties in the slopes and intercepts before you can calculate the uncertainty in the intersection. Have you studied error propagation?

 

[SuchBants]

How did you get the straight lines that you show in the figure? If you used some type of canned linear regression program, the uncertainties in the slopes should be available. In fact, as I look at your figure, there is no scatter in your data points. Why are your error bars so large?

What I mean is that if the straight lines are characterized by y = a₁x + b₁ and y = a₂x + b₂, then you should have an idea of the uncertainties in the slopes and intercepts before you can calculate the uncertainty in the intersection. Have you studied error propagation?

Yea prism has given me an error in the slope but this doesn't take into account the error bars. The data plotted is mean intervals for an oscillation. Therefore I put the uncertainty in the interval is the random uncertainty in the mean for each point. This was about 2-3% in most.

No I haven't and I don't have time to, I'm just trying to finish my project this is my final year of high school.

 

[kuruman]

As I mentioned before, it looks like your error bars at least for the time measurements are much larger than expected considering the scatter in your data. Setting that aside and since you haven't seen error propagation analysis, here is what I would suggest.
1. Make another plot of your data without the straight line fits, just the two sets of point.
2. Use a transparent ruler to draw two straight lines for each set. These should be the "bracket" lines, i.e. the lines that still provide a reasonable fit to your data but not the best fit. The four lines thus drawn will specify a quadrilateral that will have the point of intersection inside it.
3. The horizontal and vertical sizes of the quadrilateral are an estimate of the uncertainty in x and y.

 

[haruspex]

Why are your error bars so large?

Error bars express the uncertainty in the individual measurements. The error bar for one is unaffected by the other values. Choosing the bar heights can be tricky. In the present case, it does look like they have been overestimated, but you have to go with what you can justify.
When reading off values from the regression line (for purposes of decision making) one should take into account both the error bars and the goodness of fit, but offhand I forget how that is done.

For finding the intersection point, I suggest plotting a single line, being the difference of the two. This is feasible because the set of x values is the same for each. In principle it is possible then to determine an error bar for each of these difference datapoints. This still doesn't quite get there, but it does simplify things a little.

 

[kuruman]

For finding the intersection point, I suggest plotting a single line, being the difference of the two.

My inclination would be to obtain the x-coordinate of the intersection point using the fitted slopes and intercepts in the equation a₁*x_int + b₁ = a₂*x_int + b₂ and solve for x_int, then go back to either straight line equation to find y_int. Plotting the differences would work only if the data sets have points at the same values of the independent variable. This appears to be the case here so I suppose either method would work just as well.

 

[haruspex]

obtain the x-coordinate of the intersection point using the fitted slopes and intercepts in the equation a1*x_int + b1 = a2*x_int + b2 and solve for x_int, then go back to either straight line equation to find y_int.

I thought the difficulty was in finding the range (uncertainty) of x for the intercept.

 

[kuruman]

I thought the difficulty was in finding the range (uncertainty) of x for the intercept.

Do you actually mean intercept as in "straight line intercept"? I thought the difficulty was in finding the uncertainties in the x and y-coordinates of the point of intersection, {x_int, y_int}. OP mentions "intersect" which I interpreted to mean point of intersection. Perhaps OP might clarify this point.

 

[haruspex]

Do you actually mean intercept as in "straight line intercept"?

Sorry, I meant intersection. I was thinking of my approach, in which it becomes the x-intercept.

 

[SuchBants]

Do you actually mean intercept as in "straight line intercept"? I thought the difficulty was in finding the uncertainties in the x and y-coordinates of the point of intersection, {x_int, y_int}. OP mentions "intersect" which I interpreted to mean point of intersection. Perhaps OP might clarify this point.

Yes - the intersect of the two lines of best fit.

 

[SuchBants]

Maybe this will help. First is the graph here:

Next I read off the intersect of the red line for a number of estimated equilibrium positions to produce the following table:

Then calculating the intervals

I then calculated the mean of sets of intervals as shown.

Then calculating the random uncertainty in the mean:

Maybe they are so large because the final interval is so much smaller. By ignoring this reading there would be less points to plot but the uncertainty would be less.

 

[haruspex]

It does help to know what you are really trying to do - find the equilibrium point from the (y_i, t_i) data of a decaying oscillation.
Write the equation as $y=e^{-\lambda t}\sin(\omega t+\phi)+h$.
It seems to me that that you can read off the frequency quite easily and accurately. The decay rate is not hard either. (A full optimisation analysis to determine those looks impossibly hard.)
So for each t_i you can calculate $A_i=e^{-\lambda t_i}$, $S_i=\sin(\omega t_i)$, and $C_i=\cos(\omega t_i)$. I'll abbreviate s=sin(φ) and c=cos(φ).
The sum square of errors is $\Sigma(y_i-A_iS_ic-A_iC_is-h)^2$.
I will write a bar above a variable or product to denote average. E.g. $n\overline{CS}=\Sigma C_iS_i$.
Differentiating wrt c gives $\bar Y=\overline{A S}c+\overline{A C}s+h$.
Wrt φ gives $\overline{AYC}c-\overline{AYS}s=\overline{ASC}(c^2-s^2)+(\overline{AC^2}-\overline{AS^2})sc+(\overline{AS}s-\overline{AC}c)h$.
In principle, these can be solved to find c, s and h, but the mix of c and s in there makes it nasty.

 

[kuruman]

It looks like you are analyzing a Cavendish balance experiment and you are trying to find the two equilibrium positions of the suspension for the two orientations of the large external spheres. If that's the case (or even if it isn't), a way to determine the equilibrium positions from the turning points is given in the TEL-Atomic manual (for their version of balance) that you can find at this site
https://www.telatomic.com/all-produts/cavendish-balance
Click on "Manual Download" and study the discussion starting on page 10. The more turning points you use, the more accurate your determination of the equilibrium position θ_e. Also note that Equation (9) on page 13 of the manual gives you a way to estimate the uncertainty in θ_e.

 

[Juancho_chem]

It's a very important problem in chemistry. For example when you run conductimetric titrations.
You can find the answer in Miller and Miller "Statistics and chemometrics for Analytical Chemistry" subject 5.11 page 151.
Good luck!

 

[kuruman]

It's a very important problem in chemistry. For example when you run conductimetric titrations.
You can find the answer in Miller and Miller "Statistics and chemometrics for Analytical Chemistry" subject 5.11 page 151.
Good luck!

This thread is more than 3 years old. Chances are the OP has moved on.