Unclear step in "Change of variable in a multiple integral" proof

[Unconscious]

I'm studying the proof of this theorem (Zorich, Mathematical Analysis II, 1st ed., pag.136):

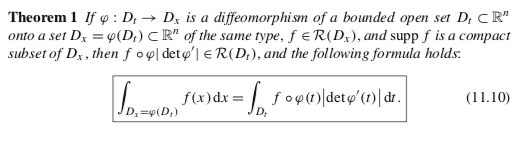
which as the main idea uses the fact that a diffeomorphism between two open sets can always be locally decomposed in a composition of elementary ones.
As a remark, an elementary diffeomorphism $\varphi$ is a diffeomorphism under which only a single variable is modified (in the following example, the last one):

$\left\{\begin{matrix} x^1=\varphi^1(t^1,...,t^n)=t^1\\ x^2=\varphi^2(t^1,...,t^n)=t^2\\ ...\\ x^{n-1}=\varphi^{n-1}(t^1,...,t^n)=t^{n-1}\\ x^{n}=\varphi^{n}(t^1,...,t^n) \end{matrix}\right.$

The proposed proof (pag.142) starts in this way:

I can't understand the last sentence, because as an intuitively counterexample I'm imagining out this situation:

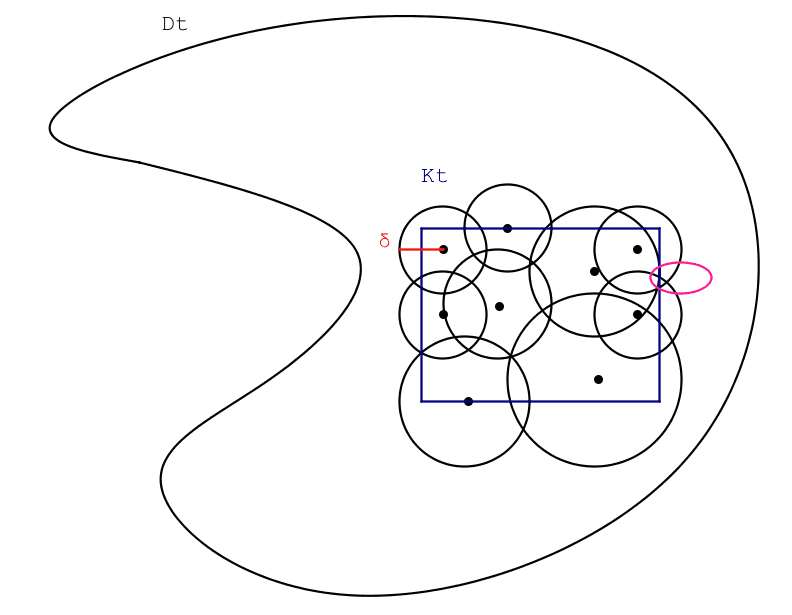
where the pink set is a set with a diameter less than $\delta$, that intersect $K_t$, but that is not contained in any neighborhoods of the finite family covering $K_t$.
Am I missing something?

 

[pasmith]

I think U(t_1), \dots, U(t_k) is meant. The truth of that is a consequence of the triangle rule, and the consequence is that any sufficiently small neighbourhood is contained within a neighbourhood where \varphi decomposes as claimed. (Compare the proof of the Heine-Cantor Theorem.)

 

[Unconscious]

Ok, the idea is clear. Thank you.

 

[Unconscious]

I post again in this thread, because I have another question on the same argument.
I'm studying this generalization (pag.145) of the previous theorem:

whose proof begins in this way:

where my doubt is on the highlighted relation.
I think that it would be $x\in\partial D_x \cup S_x$ instead $x\in\partial D_x \setminus S_x$, no?
If I'm wrong, then I can't understand the successive relation $\overline{V}_x\subset D_x\setminus S_x$, because I can't see why a point of $\partial V_x$ could not be inside $S_x$.