- #1
ChrisVer
Gold Member
- 3,378
- 464
Can someone help me understand what information we extract from such kind of figure?
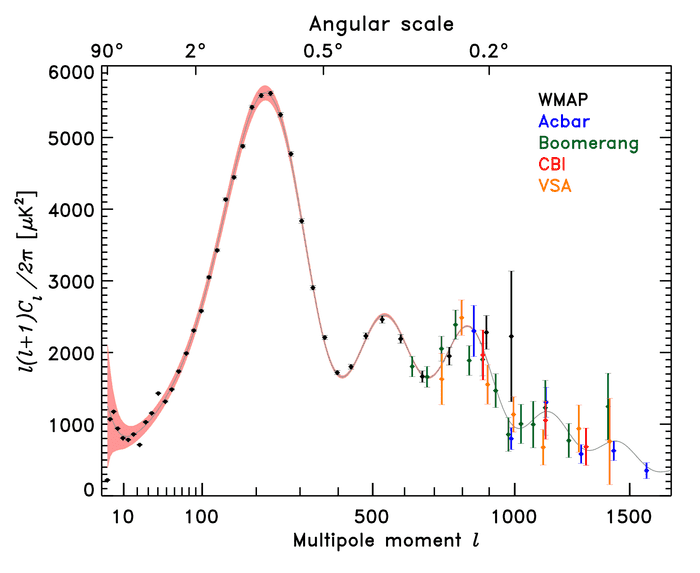
In fact the [itex]C_l^{TT}[/itex] parameter gives us information on the amplitude of the temperature fluctuations [itex]\Delta T/T[/itex]... However I don't understand why there is such a peak formation (1 very large, 2 smaller and 2 even smaller), or why this is given in terms of multipole index [itex]l[/itex].
In fact the [itex]C_l^{TT}[/itex] parameter gives us information on the amplitude of the temperature fluctuations [itex]\Delta T/T[/itex]... However I don't understand why there is such a peak formation (1 very large, 2 smaller and 2 even smaller), or why this is given in terms of multipole index [itex]l[/itex].