usermath
- 5
- 0
When I solve a quadratic equation I need to find a Discriminant. If D>0 I have no problem. I can find x1 and x2. And when I draw a parabola I can see the x1 and x2 on a X-line.
But when D<0 I don't understand where I can find x1 and x2 on a plot of function.
For example for 5x2+2x+1=0
I have complex solutions: x1 = -0.2-0.4j and x2 = -0.2+0.4j
Ok. It's the answer, but what I can do with one? Where can I find this points on the plot of function?
It's a plot of funciton y=5x2+2x+1
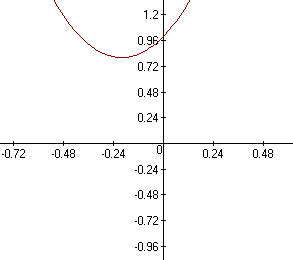
Coordinates of a Minimum Point is X = -0,2 Y = 0,8.
What does (y=0; x=-0.2+0.4) mean? How can I use this expression? Where I can find the point with coordinates y=0; x=-0.2+0.4j ?
But when D<0 I don't understand where I can find x1 and x2 on a plot of function.
For example for 5x2+2x+1=0
I have complex solutions: x1 = -0.2-0.4j and x2 = -0.2+0.4j
Ok. It's the answer, but what I can do with one? Where can I find this points on the plot of function?
It's a plot of funciton y=5x2+2x+1
Coordinates of a Minimum Point is X = -0,2 Y = 0,8.
What does (y=0; x=-0.2+0.4) mean? How can I use this expression? Where I can find the point with coordinates y=0; x=-0.2+0.4j ?