Instinctlol
- 79
- 0
Prove: For all integer n, 4 does NOT divide n2 + 5
The definition of | means the definition of divide.
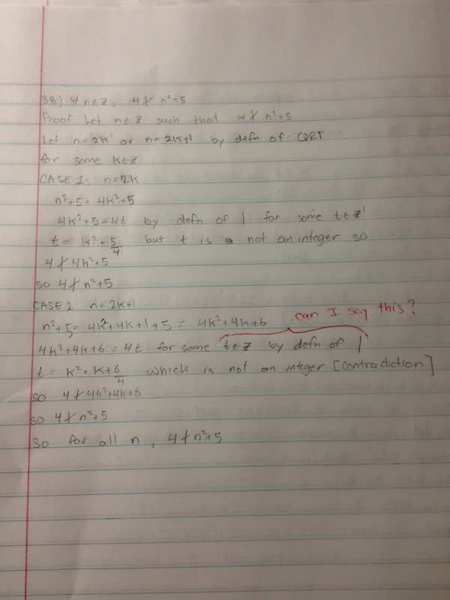
I need very thorough correction, down to the last support for every thing. Thank you
The definition of | means the definition of divide.
I need very thorough correction, down to the last support for every thing. Thank you