Understanding maximally extended Schwarzschild solution

[Hurkyl]

The no hair theorem states a black hole is completely characterized by its mass, electrical charge and angular momentum.

The no hair theorem, as I understand it talks about what quantities an external observer can measure about the black hole -- it says nothing about what an internal observer can measure. And we already see counterexamples: there's a metric inside, internal observers can look at other particles that have fallen in, etc...

Sorry you have lost me here. (Probably more my fault than yours. :P) Is there any chance of posting a sketch of a vanishing geodesic in Kruskal coordinates?

http://the1net.com/images/SK.gif
Red+Blue+Pink vanishes twice, as it runs off of the coordinate chart in different directions. (F5 and F'' don't correspond to points of space-time; aren't part of the coordinate chart)
<-- C'' - C' - C --> vanishes twice, as it runs off of the coordinate chart in different directions.
Green vanishes twice, once as it runs off of the coordinate chart, and once at F4. (F3 isn't part of the coordinate chart)

And for fun, in your Schwarzschild picture:
The green geodesic vanishes twice
The blue geodesic vanishes twice
The pink geodesic vanishes twice
(And these are all different geodesics; they are not connected)
The horizontal axis contains two different geodesics: the interval (0, 2) and the interval (2, +\infty). Both geodesics vanish as they run off of the coordinate chart at both ends.

(Yes, let me repeat that for emphasis: the point (r, t) = (2, 0) is not part of the Schwarzschild coordinates. It is part of (r, t)-space, of course, but it is not a part of the coordinate chart)

That would suggest (to me anyway) that the equation for the motion of a photon in Schwarzschild coordinates is discontinuous across the event horizon.

Yes, we already knew that: as the photon passes along the blue & pink geodesic, it passes through the point F' which is not covered by Schwarzschild coordinates.

 

[JesseM]

Which agrees with my earlier claim that all points in Schwarzschild coordinates can be transformed one for one to points in regions I and II of Kruskal-Szekeres coordinates. There is no need for regions III and IV.

Again, there's a "need" for them if you want to ensure that every possible worldline seen in region I and II does not end at finite proper time unless it hits a singularity.

Thanks for uploading the scanned diagrams. I have extended and added to the third diagram from page 825 to illustrate some important points in the diagram below:

http://the1net.com/images/SK.gif

The diagram now includes the full trajectory of a free falling particle in Schwarzschild coordinates. The trajectory is identified by events F3, F4, F, F' and F''. These points are mapped into regions I and II of the Kruskal-Szekeres coordinates. Note that the red segment (F5 to F4) which was part of the original MTW diagram does not exist in Schwarzschild coordinates. It has been added to satisfy the desire to terminate all worldlines at a singularity. However, if you look carefully you will see the trajectory already terminates at a singularity at point F3 and there is no need to add the red segment, as that part of the trajectory is already described by the dark green segment (F3 to F4).

Unless you explicitly perform some kind of topological identification like the one discussed http://casa.colorado.edu/~ajsh/schwm.html#kruskal, the dark green worldline F3 to F4 does not connect to the dark blue worldline, it's not the same particle at all! The dark green worldline represents a separate particle that fell into region II from region III (or if you remove region III, it's a particle that just appeared suddenly at an 'edge' of spacetime that is not a singularity). It may look like they connect in the Schwarzschild coordinate diagram, since both approach r=2m in the limit as t goes to -infinity, but once again you have to think in terms of the actual spacetime geometry rather than just the coordinate representation. Physicists surely have some purely geometric definition of what it means for a timelike curve to be continuous, one that doesn't depend on your choice of coordinate system. And since the Kruskal-Szekeres coordinate system is well-behaved everywhere whereas the Schwarzschild coordinate system is badly-behaved on the horizon, if we want to know about the continuity of curves which cross the horizon, I'm sure the Kruskal-Szekeres system is a better guide to what this geometric definition (whatever it is) would say about a given choice of worldline. Now, I'm not an expert in GR or differential geometry or topology so I don't know what this geometrical definition would be, though I'm confident some such definition would exist (google the phrase "continuous timelike curves" in quotes and you get a bunch of relativity papers which use the term, and the wikipedia pages on curve and continuous function may give some insight), and unless you know the definition yourself you have no basis for concluding that the green curve and the blue curve are part of single continuous curve. Does anyone else on this forum know how continuity for timelike curves is defined in GR?

The path F3, F4, F is continuous although it does not look like it in the Kruskal diagram. Point F4 appears to defined in two places in the Kruskal diagram, but they are in fact the same "place" as the diagonal line from top left to lower right is all defined by the coordinates r=2m and t=-infinity, (except at the origin of the diagram).

This is not "naturally" true unless you explicitly identify the point you've labeled F4 on the white hole horizon on the bottom right with the point you've labeled F4 on the black hole horizon on the upper left. If you don't, they represent different geometric points on the manifold, points that the Schwarzschild coordinates just can't distinguish because Schwarzschild coordinates are badly-behaved on the horizon (neither point would have a finite R and t coordinate). And if you leave out regions III and IV of the manifold, and don't do any topological identification of the edges, then both points lie on the edge of the manifold where curves just stop despite not hitting a singularity.

Perhaps this would be easier to see if you think about embedding diagrams for a series of spacelike slices through a spacetime that includes only regions I and II with no explici topological identification of the edges. As shown in this diagram from MTW, you don't have to pick horizontal lines in Kruskal-Szekeres coordinates, any spacelike slice corresponds to an embedding diagram:

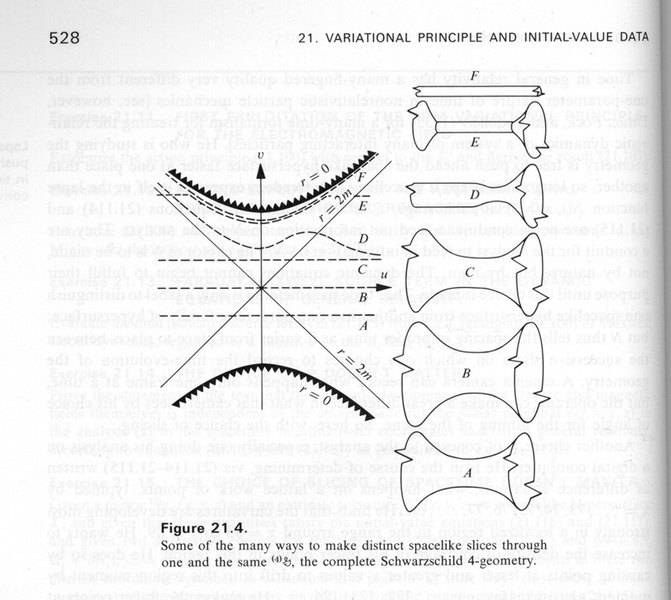
Now suppose we paint the event horizons onto the embedding diagrams based on where the spacelike slices cross the horizons, as in http://casa.colorado.edu/~ajsh/schww_gif.html posted earlier. If you simply remove regions III and IV without doing any topological identifications, then any spacelike slice which had passed through a horizon into III or IV will now simply end at the point where that horizon was painted onto the embedding diagram--the embedding diagram might look something like a tube sliced down the middle. If you perform the topological identification given http://casa.colorado.edu/~ajsh/schwm.html#kruskal which is what you seem to be doing implicitly, then effectively what you are doing is stitching together open-ended embedding diagrams from earlier spacelike slices with open-ended embedding diagrams from later slices so that each stitched-together version is a continuous surface with no abrupt edges (for example, in the MTW diagram above imagine taking a version of slice A that ends at the right 'white hole' horizon, and stitching it together with a mirror-reflected version of slice C that ends at the left 'black hole' horizon).

One disappointing aspect of the MTW drawing is that they have got the curvature of the F,F' path wrong. It should be curving the other way like the A,A' curve. The F,F' curve should look like the dotted curve in this diagram from mathpages: http://www.mathpages.com/rr/s6-04/6-04.htm

http://www.mathpages.com/rr/s6-04/6-04_files/image054.gif

[/URL]
Well, in the caption on the diagram from p. 835 they do say that the shape of the curves in the Schwarzschild diagrams is "schematic only", maybe the same is supposed to be true of the curves in the Kruskal-Szekeres diagram there. I wonder, though, if it's possible that if we consider a family of curves representing particles ejected to different maximum heights (from 2.5m in the mathpages diagram to the 5.2m in the MTW diagram), maybe the shape of the curves would smoothly vary from flexing inward to flexing outsward? There might be some intermediate height, say 3m, where the worldline of a particle that rose to that height and then fell again would just look like a vertical line in the Kruskal-Szekeres diagram. On the other hand, it may just be an error as you say.

Why do authoritative sources neglect to show the correct path for the F3,f4 segment.

Because it is not the correct one unless you perform the topological identification mentioned above. If you don't, then the green line represents an infalling particle that came from region III, its worldline is not continuous with the blue worldline of the particle falling from region I. And in this case the proper time of the green worldline should be increasing as the coordinate time t increases in the Schwarzschild diagram, at least if you want your definition of proper time to have the nice property that whenever two timelike worldlines cross at a point, they should always agree which of the two light cones emanating from that points is the future light cone of increasing proper time. In most "normal" spacetimes it's possible to define each timelike worldline's proper time in a consistent way so this will be true, but I believe that if you do the weird topological identification discussed, the only way this can work is if the proper time of either outgoing or ingoing particles is forced to suddenly reverse directions when they cross the horizon...this is a weird features of this topology which suggests that in such a universe you'd get into serious trouble if you tried to imagine both ingoing and outgoing objects as non-equilibrium systems with their own thermodynamic arrow of time and "memory".

Not one for one, exactly...the set of all points on the event horizon at r=2M and finite t in Schwarzschild coordinates actually corresponds geometrically to only a single event, and in Kruskal coordinates this event is more faithfully represented as a single point, the point at the centre where the white hole horizon meets the black hole horizon.

All free falling particles and even photons only cross the event horizon at future infinity or past infinity so that is not an issue.

That's not true, on the Kruskal-Szekeres diagram it's clear you can draw timelike worldlines that cross through the exact center of the diagram, and even light worldlines that are stuck on the horizon so they cross through the center too. If you plotted these wordlines in Schwarzschild coordinates (which would just be a matter of doing a coordinate transformation), the light worldline would just look like vertical line on the horizon, and I imagine the particle worldline would be broken up in two, one part a vertical line that stays on the horizon forever and another part a curve inside the horizon hitting the singularity at some finite time.

Sorry, I should of made it clear it was illustrating two black holes. Although Schwarzschild coordinates describe a single black hole, in an otherwise empty universe, I hope you will concede that in the real world there is more than one black hole. The diagram I posted was just an informal sketch of an old idea by Hawking about black holes ejecting matter into baby universe, but even Hawking has retracted that idea now.

OK, but the main part I was objecting to was your claim that for each individual hole, the black hole in one universe connects to a white hole in another. That's not right, any spacelike slice that contains a black hole horizon on one side contains either a black hole horizon on the other, or no horizon (see the diagram from p. 528 I posted above where slice D crosses the black hole horizon on the right side but stays between the horizon and the singularity forever on the left).

The maximally extended Kruskal solution is completely unrealistic in the real world because it's based on a black hole/white hole that has been there eternally, it never formed from a collapsing star. Note that from the outside it does not really appear as either a black hole or white hole, instead it appears as a kind of "gray hole" because an outside observer can simultaneously be watching stuff that came from region IV passing him on its way out, and at the same time be watching stuff falling in towards it that will enter into region II.

You make a very astute observation. Not many people are aware of this fact and it not widely publicized. The conventional interpretation predicts that particles can leave the black hole at the same time as particles fall in.

That's a little imprecise, in the exterior region I you can see particles passing you on their way out simultaneously with particles passing you on their way in, but the region of spacetime the outgoing particles came from (region IV) is different from the region of spacetime the ingoing particles are going to (region II), and it's convention to refer to region II as the black hole interior region and region IV as the white hole interior region.

In the conventional interpretation, particles can enter or leave the gray hole but strangely photons can only enter. Odd, that.

What do you mean by that? Both particles and photons can be emitted from region IV, I see no difference in this respect.

Take a look at this diagram from this mathpages article: http://www.mathpages.com/rr/s6-07/6-07.htm

It shows that whatever height the particle falls from, the acceleration is always zero at the event horizon r=2m. This is the Schwarzschild coordinate acceleration.

Sure, but that's just a coordinate acceleration, it's no more physical than the coordinate acceleration as you cross the horizon in Kruskal-Szekeres coordinates, which need not be zero. So what physical point are you trying to make here? Do you agree that no matter what coordinate system we use, the proper time to reach the event horizon along a timelike curve (setting its clock to zero at some finite radius) will be finite? Note that the square of the proper time along a curve is just the integral of ds^2 along that curve times the constant -(1/c^2). Also, do you agree that physicists surely have some coordinate-independent geometric definition of what it means for a timelike curve to be continuous, and that presumably it's possible to verify that even in Schwarzschild coordinates the curve representing the infalling particle outside the horizon meets up continuously with the curve representing the same infalling particle inside the horizon?

The acceleration in proper time at the event horizon might be infinite but that is not surprising if the observer is using a stopped clock.

What do you mean by "acceleration in proper time"? If you're talking about proper acceleration, i.e. acceleration as measured in the object's instantaneous local inertial rest frame at a particular moment (which is the acceleration they'd feel as G-forces), then if we're talking about a particle following a geodesic the proper acceleration is always zero at every point on their worldline.

Something to ponder: It is easy to show that a photon can stationary at the event horizon. Agree or disagree?

"Stationary" in Schwarzschild coordinates but not in Kruskal-Szekeres coordinates, and more physically, still measured to move at c in the locally inertial frame of a freefalling observer crossing the horizon (because in this locally inertial frame, the horizon itself is moving outsward at a speed of c).

 

[knobsturner]

To everyone who posted - thanks.

I have one question / thing to add. If we have in some hypothetical universe, a 'real' maximally extended Schwarzschild solution, what happens when we toss in some mass in one side? I mean what happens to the _masses_. Say the soln is for mass M and you toss in M/3 into one side. It would then seem that since information can't get to the 'other side', the other side will stay with a mass of M, while this side would be 1.33M.

What does a Kruskal diagram look like when you have M on one side, and say 1.33M on the other? Put another way - if you draw 2 Kruskal diagrams with different masses, is there a way to cut them (eg along some coordinate axis, etc) so that one 'dual mass' drawing would be the result?

It might seem that an entirely new solution of the GR equations would be needed, but since there is no information passed - it is not obvious how each side could be different from the static solution. But if there is a curvature discontinuity of some sort, then the door is open to communicate through the hole, by playing with the mass of the hole.

 

[yuiop]

..
Well, in the caption on the http://www.jessemazer.com/images/p835Gravitation.jpg" they do say that the shape of the curves in the Schwarzschild diagrams is "schematic only", maybe the same is supposed to be true of the curves in the Kruskal-Szekeres diagram there. I wonder, though, if it's possible that if we consider a family of curves representing particles ejected to different maximum heights (from 2.5m in the mathpages diagram to the 5.2m in the MTW diagram), maybe the shape of the curves would smoothly vary from flexing inward to flexing outsward? There might be some intermediate height, say 3m, where the worldline of a particle that rose to that height and then fell again would just look like a vertical line in the Kruskal-Szekeres diagram. On the other hand, it may just be an error as you say...

Here is a Kruskal-Szekeres diagram on which I have plotted a family of free falling particle trajectories with apogees at r = 2.001M, 2.1M, 2.5M, 3.0M, 3.5M and 4.0M respectively:

http://the1net.com/images/KT.gif

The light blue curves are the complete Schwarzschild trajectories transformed to K-S coordinates. The curves are not just some sort of artists impression, but are plotted from equations using graphical software. The yellow curves are copies of the particles and their trajectories in some sort of parallel possibly imaginary) universe.

The trend is clear. The curves go from being a straight vertical line at the origin of the KS coordinates to curving more strongly outwards as the apogee gets further away from the event horizon. In other words they curve in the opposite direction to the F.F' curve shown in the MTW drawing. Now I don't think MTW are in the habit of making such gross mistakes, so we we will have to assume that the F,F' curve is the path of an object that is being artificially accelerated inwards such as a rocket. To be fair to MTW they do not claim it is the path of a free falling particle, but perhaps they should of made it clear it is not. On the other hand, the A,A',A'' path in the MTW diagram would appear to be the correct depiction of a free falling particle in Schwarzschild and KS coordinates, with the observation that the apogee of that particle is not placed at the usual t=0, but there is nothing that says it has to be.

 

[yuiop]

No they don't. You're identifying points all over the place; you assert the green and red segments cover the same trajectory, and that all of the points on the v=-u diagonal are actually the same "place".

In the maximal extended solution, if two points have different Kruskal-Szekeres coordinates, then they are different points.

I claimed the green segment in http://the1net.com/images/SK.gif" is the transformation of the green segment in the Schwarzschild diagram. The red segment is an arbitrary copy of the green segment in a supposed parallel universe. The second copy of the segment comes about by giving reality to the fact that a square root has two roots, one positive and one negative. For example the length of the diagonal of a right angled trangle has a positive and negative solution and so does the proper time of an object with relative motion but we know from experience that the only the positive root has physical significance in those cases. Maybe in some parallel universe the proper time of a moving object is running backwards relative to the proper time of the copy of the object in our universe.


As for my other claim that the two copies of F4 on the u=-v diagonal of the SK diagram are the same "place" I present the folowing argument. In the diagram below I have made a cut along the u=v axis and rotated region II down to where region IV normally is and glued the two u=-v edges to make some arbitrary rotated version of the normal KS coordinates.


http://the1net.com/images/F4.gif

In the rotated diagram, F4 is unambiguously one place and now it is F' that appears to be in two diffent places but that is obviously just an artifact of where I chosen to make a cut. In the same way, F4 appears to be two different places in normal KS coordinates because it happens to be on the line where the cut is made, in those coordinates.

The yellow lines are future light cones. It can be seen that whatever coordinates you choose the particle moving along the segment F3,F4 is unambiguously moving backwards in time as it moving from its future light cone to its past light cone. As the particle (or photon) travels backwards in time it has to arrive at past infinity before it can cross from region II into region III, but because the big bang is not in the infinite past that option is not open and the particle can not move from region II to region III and a similar argument means a particle or photon can not move from region IV to region I or vice versa. Regions III and IV are completely cut off from our universe (regions I and II) if our universe has only existed for a finite time since the big bang. I think that answers one the questions you posed in your opening post. It also solves the problem of the requirement of all worldlines to terminate at a singularity without introducing regions III and IV because the big bang counts as a singularity.

http://the1net.com/images/PBB.gif

The black triangular regions in the above diagram is time before the big bang going back to past infinty. It effectively cuts off regions I and II from regions III and IV and so regions III and IV have no physical significance in our universe with a finite past.

However, it might be argued that a particle falls into a black hole (or is emitted) in finite proper time and if we take proper time as somehow more physically real than coordinate time, then fact that the universe probably does not have an infinite past is not a problem, but that requires that the trajectory in proper time does not have a corresponding trajectory in coordinate time. For me, if the path does not exist in all possible valid coordinate systems, then it is not a physically real path. This sort of relates to an interesting question posted in this thread by Mentz, that no one has attempted to answer yet.

 

[George Jones]

This thread is very interesting. I have a question about ontological status and coordinate transformations in GR.

If a phenomemon P is predicted by one set of coordinates, but not by another, is that enough to say that P cannot be physical, but is observer dependent ?

It depends on what you mean by "phenomena," "set of coordinates," and observer." Can you (Mentz) give an example of what you have in mind?

 

[JesseM]

I claimed the green segment in http://the1net.com/images/SK.gif" is the transformation of the green segment in the Schwarzschild diagram. The red segment is an arbitrary copy of the green segment in a supposed parallel universe. The second copy of the segment comes about by giving reality to the fact that a square root has two roots, one positive and one negative. For example the length of the diagonal of a right angled trangle has a positive and negative solution and so does the proper time of an object with relative motion but we know from experience that the only the positive root has physical significance in those cases. Maybe in some parallel universe the proper time of a moving object is running backwards relative to the proper time of the copy of the object in our universe.

The second copy of the segment does not come about simply because the square root has two solutions, once again you fail to distinguish coordinate-based statements from geometric ones. It's not true in every coordinate system that regions III and IV lie exclusively at negative values of the spatial coordinate, in fact this isn't even true in Kruskal-Szekeres coordinates (parts of region IV have positive values). The extra regions III and IV are needed for geometric reasons, to make the spacetime be "maximally extended". Any geometric definition of the identity of points will show that the two points you label F4 lie at different locations on the manifold, they are not the same point unless you do an explicit topological identification. And like I said, if you actually were to calculate the embedding diagram through a spacelike slice that cuts out regions III and IV, like a horizontal line which meets the lower point labled F4 in your diagram, then you'd get an embedding diagram that has an "edge", like a wormhole embedding diagram that's been sliced down the middle...the only way to avoid this is, again, a topological identification that stitches together the embedding diagram from the horizontal line that goes through the lower F4 in your diagram with a different embedding diagram, like the horizontal line going through the upper F4 in your diagram.

As for my other claim that the two copies of F4 on the u=-v diagonal of the SK diagram are the same "place" I present the folowing argument.

You're going into crackpot territory if you keep pushing this "claim", you can't just make intuitive arguments for why you think they "should" be the same place, which points are identical is not some subjective handwavey issue, I'm sure it's a well-defined geometric issue. It'd be as if I had had a coordinate system and metric representing the top half of a globe (everything above the equator), and someone pointed out that to prevent geodesics from just cutting off we'd need the region connected to another one representing the bottom of the globe below the equator, and I said this wasn't necessary, because the point labeled the South Pole on the other diagram was "really" just the same as the point at the North Pole in the original diagram, and presented some handwavey argument as to why this "should" be. The fact would remain that if you calculated the embedding diagram for the metric in the coordinate system, it'd look like a hemisphere rather than a full sphere, and if we looked at the two hemispheres as represented in a different coordinate system which could represent the full surface, geometrically the North Pole would be a different point on the manifold than the South Pole, unless I explicitly add the assumption of a topological identification of the two regions.

In the rotated diagram, F4 is unambiguously one place and now it is F' that appears to be in two diffent places

Um, only because when you did the rotation, you didn't keep the names of the points the same as would be naturally, instead you changed the names of the points F4 to F'. A mere visual rotation of a graph shouldn't change the identity of points on a manifold being graphed!

The yellow lines are future light cones. It can be seen that whatever coordinates you choose the particle moving along the segment F3,F4 is unambiguously moving backwards in time as it moving from its future light cone to its past light cone.

Only because you chose to draw its arrow pointing downwards, which is not how it's usually depicted. Since the laws of physics are time-symmetric it's essentially just a matter of convention which direction on a curve is increasing proper time and which is decreasing proper time, but as I said, it's more normal to assign these directions in such a way as to make sure they all agree:

And in this case the proper time of the green worldline should be increasing as the coordinate time t increases in the Schwarzschild diagram, at least if you want your definition of proper time to have the nice property that whenever two timelike worldlines cross at a point, they should always agree which of the two light cones emanating from that points is the future light cone of increasing proper time. In most "normal" spacetimes it's possible to define each timelike worldline's proper time in a consistent way so this will be true, but I believe that if you do the weird topological identification discussed, the only way this can work is if the proper time of either outgoing or ingoing particles is forced to suddenly reverse directions when they cross the horizon...this is a weird features of this topology which suggests that in such a universe you'd get into serious trouble if you tried to imagine both ingoing and outgoing objects as non-equilibrium systems with their own thermodynamic arrow of time and "memory".

You can see that in the normal way of depicting increasing proper time of worldlines in a Kruskal diagram shown http://casa.colorado.edu/~ajsh/schww.html, they are drawn in such a way that at every crossing-point both worldlines do agree on which light cone is the future one:

On the other hand, if you do the topological identification discussed http://casa.colorado.edu/~ajsh/schwm.html#kruskal, where regions IV and III are defined to be the same as regions I and II (shown as upside-down mirror images in the Kruskal-Szekeres diagram), then in order to make sure that crossing worldlines still agree on the direction of future light cones both inside and outside the horizon, you have to have some of the worldlines switch their direction of increasing proper time on the horizon (note that in the bottom region IV of the diagram the dark orange worldlines have arrows pointing downwards, but on the right region I the dark orange worldines have arrows pointing upwards):

As the particle (or photon) travels backwards in time it has to arrive at past infinity before it can cross from region II into region III, but because the big bang is not in the infinite past that option is not open and the particle can not move from region II to region III and a similar argument means a particle or photon can not move from region IV to region I or vice versa. Regions III and IV are completely cut off from our universe (regions I and II) if our universe has only existed for a finite time since the big bang. I think that answers one the questions you posed in your opening post.

"Past infinity" of what? Schwarzschild coordinates? You still seem to privilege Schwazschild coordinates over other coordinate systems for no good reason, and you never really respond to my constant harping about the distinction between geometric statements which are the same in all coordinate systems and truly "physical", and mere coordinate-based statements which are not...do you agree or disagree with this distinction? Also, of course there is no Big Bang in the Schwarzschild geometry, the Schwarzschild geometry describes an eternal black/white hole in an asymptotically flat universe (no expansion of space), so your comments above are totally confused...I doubt that you could even find a spacetime geometry featuring the same sort of black hole/white hole combination in a more realistic universe which began at some finite point in the past with a Big Bang.

 

[JesseM]

This thread is very interesting. I have a question about ontological status and coordinate transformations in GR.

If a phenomemon P is predicted by one set of coordinates, but not by another, is that enough to say that P cannot be physical, but is observer dependent ?

Sorry, forgot about this. I would say it's definitely true that any geometric fact which is predicted by all coordinate systems, like the integral of ds^2 along a curve (which for timelike curves is just the square of the proper time multiplied by -c^2) is a physical truth. As for whether coordinate-based truths can also be physical, I'd say only in the limited sense that if you can construct a system of rulers and clocks whose local readings next to events match those of the coordinate system, then in that sense a coordinate-based truth can be transformed into a coordinate-independent physical truth.

 

[Mentz114]

George,

It depends on what you mean by "phenomena," "set of coordinates," and observer." Can you give an example of what you have in mind?

Are 'observers' and 'coordinates' the same thing ? I.e. a frame ? I suppose by 'phenomenon' I mean any observable.

The two things that spring to mind are 1) matter falling into a black hole and 2) the singularity at r=0 ( which in Kev's coordinates does not exist except at infinite time).

JesseM:

I would say it's definitely true that any geometric fact which is predicted by all coordinate systems, like the integral of ds^2 along a curve (which for timelike curves is just the square of the proper time multiplied by -1/c^2) is a physical truth. As for whether coordinate-based truths can also be physical, I'd say only in the limited sense that if you can construct a system of rulers and clocks whose local readings next to events match those of the coordinate system, then in that sense a coordinate-based truth can be transformed into a coordinate-independent physical truth.

Good point. I suppose for something to be real we must be able (in principle) to imagine an observer to measure it.

Obviously there's no simple answer.

 

[yuiop]

...
As for my other claim that the two copies of F4 on the u=-v diagonal of the SK diagram are the same "place" I present the folowing argument. In the diagram below I have made a cut along the u=v axis and rotated region II down to where region IV normally is and glued the two u=-v edges to make some arbitrary rotated version of the normal KS coordinates.

You're going into crackpot territory if you keep pushing this "claim", you can't just make intuitive arguments for why you think they "should" be the same place, which points are identical is not some subjective handwavey issue, I'm sure it's a well-defined geometric issue.

There is nothing handwavey about the mathematical fact that all points along the u=-v diagonal (except for the point at the origin) have the same Schwarzschild coordinates (r=2m and t=-infinity). That single point in Schwarzschild coordinates has been stretched into a line in the KS metric. It's a bit like the points marked a,b and c on the mercator projection of the global map below are all the same place (the North pole) but they appear to be spatially separated along the North edge of the projection. That is a good example of a single point being streched out into a line as a consquence of transforming from one set of coordinates (the curved surface of a sphere) to another (a flat chart).

http://the1net.com/images/world-map.gif

I have also labelled a point as F4. On the left map it appears to be two separate places but if the cut is made along a different line of longitude it becomes clear that F4 is a single point in a single place and now it appears like point F' is in two separate places on the second map. This appearance of a single point appearing to be in two spatially separated places is clearly an artifact of where we choose to make the cut. Obviously we are dealing with purely spatial (x,y) coordinates here while in the Schwarzschild and KS coordinates we are dealing with space and time (r,t) coordinates, but it is a good analogy. Also, it should be noted that in the mercator projections it is not immediately obvious that the two dark blue paths on each map are a continuous (and shortest) path from South America to Australia. This is an anology to my claim that the green segment (F3 to F4) and the blue segment (F4 to F) in http://the1net.com/images/SK.gif" is one continuous path although it is not obvious in KS coordinates.

Um, only because when you did the rotation, you didn't keep the names of the points the same as would be naturally, instead you changed the names of the points F4 to F'. A mere visual rotation of a graph shouldn't change the identity of points on a manifold being graphed!

The names of the points were never changed! Have a close look

Only because you chose to draw its arrow pointing downwards, which is not how it's usually depicted. Since the laws of physics are time-symmetric it's essentially just a matter of convention which direction on a curve is increasing proper time and which is decreasing proper time, but as I said, it's more normal to assign these directions in such a way as to make sure they all agree:

Arrows are not normaly drawn on these types of diagrams and I have added them to make it clear what is going on. The arrows represent where the particle is traveling to. Either the particle traveling from F3 to F4 is traveling from the central singularity to the event horizon or it not. When the path is plotted in parametric form as described by mathpages here the direction becomes clear because the parametric variable defines how the curve evolves. In Schwarzschild coordinates the particle is traveling backwards in time (from future light cone to past lightcone) and in Kruskal-Szekeres coordinates it is clearly also traveling from future to past as defined by the lightcones. Now I grant you that the while the particle is traveling backwards in Schwarzschild coordinate time, that its proper time is advancing normally. However, I question why we always give priority to proper time over coordinate time? Is proper time a good arbitrator of what is physically real? I think it is not. For example in the traditional twins thought experiment, both twins experience their individual proper times as advancing normally at the rate of one second per second and each measures the other twins clock to be running slower than their own clock, but when they get back together they find one has actually aged less than the other. Proper time is poor measure of what is really physically happening in my opinion.

... You still seem to privilege Schwazschild coordinates over other coordinate systems for no good reason, and you never really respond to my constant harping about the distinction between geometric statements which are the same in all coordinate systems and truly "physical", and mere coordinate-based statements which are not...do you agree or disagree with this distinction?

I do understand and agree with the distinction and yes it is my belief that the Schwarzschild metric is a correct solution of General Relativity.

 

[Hurkyl]

Suppose I decided to draw the attached map of the world. Would I be justified in saying that Mexico and Canada actually border each other, because every point of 90° West longitude has the same coordinates, and thus must be the same point?



(r, t) = (2Gm, -infinity) fails to be a point in a Schwarzschild coordinate chart for two reasons:
(1) t is not a real number
(2) r is not in the domain of either the exterior (2Gm < r) Schwarzschild chart or the black hole (0 < r < 2Gm) chart

And whether or not multiple points of a manifold have the same coordinates in some representation is completely and utterly irrelevant. The manifold is what matters, not the representation; if multiple points have the same coordinates in some representation, then that is simply a failure of the representation to faithfully describe the manifold.

 

[JesseM]

There is nothing handwavey about the mathematical fact that all points along the u=-v diagonal (except for the point at the origin) have the same Schwarzschild coordinates (r=2m and t=-infinity). That single point in Schwarzschild coordinates has been stretched into a line in the KS metric.

What's handwavey is that you're talking as though it's a he said/she said situation and we can pick whichever picture we like better. It's not, there are geometric facts about whether points that have different coordinates in one system but the same coordinates in another really represent the same geometric point in the manifold or not. And in this respect, any textbook discussion of the subject will tell you it's Schwarzschild coordinates that distort things by stretching single events into lines (specifically the event at the middle of the Kruskal-Szekeres diagram) and pushing distinct events off to infinity, while Kruskal-Szekeres coordinates accurately represent distinct physical events (distinct geometric points on the manifold) as different coordinates. This isn't something physicists just decided arbitrarily because they like Kruskal-Szekeres diagrams better, I'm sure it is possible to check this using geometric definitions of what it means for distinct points in a coordinate representation to actually denote a single geometric point, or what it means for a coordinate path to represent a continuous geometric curve on the manifold, and verify that it's Kruskal-Szekeres diagrams that in fact represent distinct points and continuous curves accurately, not Schwarzschild coordinates.

By the way, just to make it a little more intuitive that it's Schwarzschild coordinates that are misleading about the geometry at the horizon, consider the wordlines of two particles that are dropped into a black hole at different times, perhaps one years after the other. In real physical terms they don't cross paths at the event horizon, but in Schwarzschild coordinates both crossing-events would have coordinates r=2M and t=+infinity. The Kruskal-Szekeres diagram will show them crossing the horizon at different points.

It's a bit like the points marked a,b and c on the mercator projection of the global map below are all the same place (the North pole) but they appear to be spatially separated along the North edge of the projection. That is a good example of a single point being streched out into a line as a consquence of transforming from one set of coordinates (the curved surface of a sphere) to another (a flat chart).

Yes, that's a very good example. Suppose we are comparing a map that stretches the North Pole into a line with another map projection that keeps it as a single point. If someone was arguing that he thought the mercator projection was "really" the more physically accurate one, and that the North Pole really was a line, what would you say to him? "There's no accounting for taste?" But clearly it is not just a matter of aesthetic preference or handwavey arguments whether the North Pole is a line or a point, in geometric terms it really is a single point on the manifold, and presumably someone well-versed in differential geometry would have a mathematical definition of a point that would allow him to see that, even when working with the metric in the coordinates of Mercator projection, the North Pole is "really" a point. Similarly, there is a real objective truth about whether distinct points in some spacetime coordinate system with an associated metric are really the same geometric point or not, I'm sure this has been investigated and all the textbooks aren't wrong when they say it's Schwarzschild coordinates that distort things while Kruskal-Szekeres coordinates accurately show different events as happening at different coordinates, and single events as happening at a single set of coordinates.

The names of the points were never changed! Have a close look

So you mean it wasn't just a rotated picture of the same spacetime region, but that the first diagram showed region I and II while the second diagram showed region I and IV?

Arrows are not normaly drawn on these types of diagrams and I have added them to make it clear what is going on. The arrows represent where the particle is traveling to. Either the particle traveling from F3 to F4 is traveling from the central singularity to the event horizon or it not. When the path is plotted in parametric form as described by mathpages here the direction becomes clear because the parametric variable defines how the curve evolves.

There isn't any physical truth about which direction along its worldline a particle is "traveling through time", if that's what you mean. Any curve can be parametrized in either direction--for example, a worldline between the horizon and the singularity can be parametrized in such a way that the parameter increasing as you move closer to the singularity along the worldline, or it can be parametrized in such a way that the parameter is increasing as you move closer to the event horizon along the worldline. Both the direction of increasing proper time and the direction of increasing parameter in a parametrization (and proper time can be used as a parameter) are simply matters of convention, though as I said it is usually convenient to define the proper time of different worldlines so that whenever two cross, they both agree on which light cone is the future one of increasing proper time.

However, I question why we always give priority to proper time over coordinate time? Is proper time a good arbitrator of what is physically real?

The direction of increasing proper time is a matter of convention, but the proper time interval between two points on a worldline is a coordinate-independent fact that all frames agree on, it's just as geometric as ds^2 (in fact if you take the square of the proper time along a timelike worldline between two points and multiply it by -c^2, that gives you the integral of ds^2 along the same worldline between those same points).

I think it is not. For example in the traditional twins thought experiment, both twins experience their individual proper times as advancing normally at the rate of one second per second and each measures the other twins clock to be running slower than their own clock, but when they get back together they find one has actually aged less than the other. Proper time is poor measure of what is really physically happening in my opinion.

Uh, what do you think physicists mean when they say "one has actually aged less than the other"? They just mean that if you compare the proper time along each worldline between the event of the twins departing and the event of the twins reuniting, one has experienced less proper time!

Proper time in spacetime is a lot like distance along a curve in 2D euclidean space, as measured by something like an odometer. First of all, they're both equally geometric. Secondly, just as a straight line between two points on a 2D plane always has a shorter distance than some curvy non-straight line between those same two points, so a straight worldline of unchanging velocity between two events in 4D Minkowski spacetime always has a larger proper time than any other worldline between the same two events. This is, in fact, a very good way of understanding the twin paradox in geometric, frame-independent terms.

I do understand and agree with the distinction and yes it is my belief that the Schwarzschild metric is a correct solution of General Relativity.

So you'd agree that there's a difference between the Schwarzschild geometry (i.e. a particular 'shape' of curved spacetime) and the Schwarzschild coordiante systems, that we are free to represent the Schwarzschild geometry in any coordinate system we like (as long as we adjust the equations of the metric to that coordinate system so all calculations of ds^2 along curves come out the same), including Kruskal-Szekeres coordinates? And do you agree that physicists surely must have geometric definitions of what it means for distinct sets of coordinates to actually represent the same geometric point in the manifold, and definitions of what it means for a coordinate representation of a curve to actually be a continuous curve in the manifold?

 

[Mentz114]

Kev: I dont't think, on reflection, you can mean this

For example in the traditional twins thought experiment, both twins experience their individual proper times as advancing normally at the rate of one second per second and each measures the other twins clock to be running slower than their own clock, but when they get back together they find one has actually aged less than the other. Proper time is poor measure of what is really physically happening in my opinion.

My bold.

But they actually aged according to what was on their clocks - so that is what physically happened ! In this case the proper times are exactly in correspondence to the physical reality. Proper time is a relativistic invariant, all observers agree on it.

 

[Suede]

How about understanding the original Schwarzschild solution first.


On the Gravitational Field of a Mass Point According to Einstein’s Theory
K. Schwarzschild, Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.) 1916 (1916) 189-196

Since I'm not a practicing theoretical physicist, perhaps someone can tell me how this:

is derived from this:
http://www.sjcrothers.plasmaresources.com/schwarzschild.pdf"

 

[stevebd1]

How about understanding the original Schwarzschild solution first.

On the Gravitational Field of a Mass Point According to Einstein’s Theory
K. Schwarzschild, Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.) 1916 (1916) 189-196

Since I'm not a practicing theoretical physicist, perhaps someone can tell me how this:

is derived from this:
http://www.sjcrothers.plasmaresources.com/schwarzschild.pdf"

To my knowledge, the Schwarzschild radius can be derived from the escape velocity equation-

v_e=\sqrt{2Gm/r}

replace v_e with c (speed of light)

c=\sqrt{2Gm/r}

rearrange relative to r-

c^2=\frac{2Gm}{r}

r_s=\frac{2Gm}{c^2}

r_s being the Schwarzschild radius, the point where the escape velocity exceeds the speed of light.

 

[yuiop]

But they actually aged according to what was on their clocks - so that is what physically happened ! In this case the proper times are exactly in correspondence to the physical reality. Proper time is a relativistic invariant, all observers agree on it.

Your right and I expressed myself very badly there. What I was trying to get at with the twins experiment, is that proper time can slow down in a real sense relative to other clocks with relative motion (or at a different gravitational potentials), as can be verified by bringing the clocks back together again. Given that proper time can vary relative to other clocks, I have to question why proper time is always given priority over coordinate time when they appear to be in conflict. For example if a particle is dropped into a black hole we could calculate that it takes for 10 minutes of the particle's proper time to arrive at the event horizon and a total of 15 minutes of its proper time to arrive at the central singularity, but is that what really happens? Does the particle actually arrive at the central singularity?

In coordinate time we calculate that it takes infinite time to even arrive at the event horizon. If we give physical significance to coordinate time (which closely approximates time measured by a clock on Earth) then the black hole will have evaporated before the particle even arrives at the event horizon. From the coordinate point of view, the particle could never have arrived at the central singularity while the black hole existed.

Next, I have to question why its OK for a particle (or observer) to travel backwards in coordinate time as long as its/his/her proper time is advancing? Why can't we take the opposite point of view and give priority to coordinate time and say motion only occurs in the direction of advancing coordinate time? After all, we can show that the proper time of a particle can slow down relative to other clocks. As for whether the proper time of a particle actually stops at the event horizon that is difficult to say, but that issue can be avoided if we take coordinate time seriously and say the particle never actually arrives at the event horizon and just approaches it asymptotically as coordinates time goes towards future infinity. I am very aware that my point of view is not the textbook point of view, but I am asking if there is the possibility of other equally valid physical interpretations of the equations of General Relativity?

 

[yuiop]

Suppose I decided to draw the attached map of the world. Would I be justified in saying that Mexico and Canada actually border each other, because every point of 90° West longitude has the same coordinates, and thus must be the same point?

That is good example of how incorrectly interpreting a chart can result in unphysical conclusions. The correct way to interpret your chart is that the point at the centre represents multiple coordinates (same longitude, multiple latitudes) which is similar to how the point at the origin of the Kruskal-Szekeres chart represents multiple coordinates (same spatial coordinate, r=2gm and many time coordinates, -infinity<t<infinity).

(r, t) = (2Gm, -infinity) fails to be a point in a Schwarzschild coordinate chart for two reasons:
(1) t is not a real number
(2) r is not in the domain of either the exterior (2Gm < r) Schwarzschild chart or the black hole (0 < r < 2Gm) chart

If (2gm, -infinity) is not part of the Schwarzschild chart then it would seem that it is not part of Eddington-Finkelstein coordinates or Kruskal-Szekeres coordinates because they are simply transformations of the Schwarzschild coordinates. Although you describe the Schwarzschild interior solution as two charts it is described by a single metric.

And whether or not multiple points of a manifold have the same coordinates in some representation is completely and utterly irrelevant. The manifold is what matters, not the representation; if multiple points have the same coordinates in some representation, then that is simply a failure of the representation to faithfully describe the manifold.

Your distorted bowtie worldmap, the Mercator projection and a globe map are all valid representations of the surface of the Earth, but they have to be interpreted carefully and we can always check the interpretations by inspection of the real world. Things are not so easily resolved when we have no way to directly measure what is happening, such as exactly at the event horizon or below the event horizon. Without the physical object to make a direct comparison to, I don’t think you could detrmine which is the correct representation. Without the prior knowledge of the physical object all three might be representations of a flat double sided triangle and the Mercator projection and the globe map would then be distortions of the triangle. There can often be more than one interpretation of mathematical solutions and sometimes, all we can do is check that the physical implications of our interpretations are physically reasonable. I can not help but think that the conventional interpretation that concludes that there is a point with zero spatial dimensions, finite mass and infinite density at the centre of a black hole is not physically reasonable..

 

[Hurkyl]

If we give physical significance to coordinate time

Why would we do such a silly thing?

is that proper time can slow down in a real sense relative to other clocks with relative motion (or at a different gravitational potentials),

Or for absolutely no reason at all. By choosing the appropriate coordinate chart, the time dilation experienced by clocks can be made to be just about anything at all; the only limitation on your freedom to do so is the constraint imposed by

bringing the clocks back together again.

why proper time is always given priority over coordinate time when they appear to be in conflict.

How can they be in conflict?

I am very aware that my point of view is not the textbook point of view, but I am asking if there is the possibility of other equally valid physical interpretations of the equations of General Relativity?

Then ask your question in another thread, and stop hijacking mine.

 

[Hurkyl]

That is good example of how incorrectly interpreting a chart can result in unphysical conclusions.

Right. And it's one of the things you're doing with the maximally extended Schwarzschild solution.

which is similar to how the point at the origin of the Kruskal-Szekeres chart represents multiple coordinates (same spatial coordinate, r=2gm and many time coordinates, -infinity<t<infinity)

Right; and pretending that one point is actually many, because Schwarzschild coordinates say so, is another of the things you're doing.

If (2gm, -infinity) is not part of the Schwarzschild chart then it would seem that it is not part of Eddington-Finkelstein coordinates or Kruskal-Szekeres coordinates because they are simply transformations of the Schwarzschild coordinates.

This is blatantly false!

Although you describe the Schwarzschild interior solution as two charts it is described by a single metric.

Sure. Given any two disjoint manifolds with a metric, there union is also a manifold with a metric.

I should point out that on the entirety of the r>0 region in (r, t) space, ds is not a metric.

Your distorted bowtie worldmap, the Mercator projection and a globe map are all valid representations of the surface of the Earth but they have to be interpreted carefully and we can always check the interpretations by inspection of the real world but things are not so easily resolved when we have no way to directly measure what is happening exactly at the event horizon or below the event horizon.

What difficulty? We have a completely defined mathematical object, and we're asking extremely straightforward questions of it. Why the heck are you talking about things like "inspection of the real world"?

 

[Hurkyl]

This is blatantly false!

I should clarify -- this is blatantly false in the situation at hand. If, instead of the topic of this thread, we were instead considering a manifold (isometric to the one) defined by the r &gt; 0, r \neq 2Gm region of (r,t)-space, then yes, Kruskal-Szekeres coordinates would indeed simply be a transformation of Schwarzschild coordinates. And the domain of KS coordinate chart would be the set
v^2 - u^2 < 1
u + v > 0
u \neq v

But that's not the manifold we're studying. The topic of this thread is the maximally extended Schwarzschild solution. And that manifold is (isometric to) the one defined by the entire v^2 - u^2 < 1 region of (u, v) space.

 

[JesseM]

Your right and I expressed myself very badly there. What I was trying to get at with the twins experiment, is that proper time can slow down in a real sense relative to other clocks with relative motion (or at a different gravitational potentials), as can be verified by bringing the clocks back together again.

Are you talking about a clock being objectively slowed relative to another at a particular moment? If so that doesn't make sense, at any given point on a twin's worldline we can pick different inertial frames which disagree about whether his clock is ticking slower or faster than his brother's clock at that moment, and yet every inertial frame will agree on the total time elapsed on each clock (the proper time) when they reunite. I posted an analogy with paths in 2D Euclidean geometry here if you're interested.

Given that proper time can vary relative to other clocks, I have to question why proper time is always given priority over coordinate time when they appear to be in conflict. For example if a particle is dropped into a black hole we could calculate that it takes for 10 minutes of the particle's proper time to arrive at the event horizon and a total of 15 minutes of its proper time to arrive at the central singularity, but is that what really happens? Does the particle actually arrive at the central singularity?

Yes, GR is a geometric theory, coordinate systems in curved spacetime have no more significance than coordinate systems on curved 2D surfaces like the surface of a sphere. No doubt we could come up with a coordinate system on a sphere where the coordinate distance between the equator and the North Pole is infinite, would this cause you to worry that a traveler might never actually reach the North Pole?

Speaking of coordinate systems, I was thinking a little more about the example of the North Pole being expanded into a line in a Mercator-like projection, and how you could show even in this coordinate system that the North Pole is "really" a geometric point. The basic idea is that every coordinate system on a surface is associated with a metric that defines a geometric, coordinate-independent notion of distance along a curve on that surface (ds^2 in spacetime, but just ordinary spatial distance when we're dealing with a metric on a 2D space). So, take any two points on the top edge of the map that are on the North Pole, draw a line between them, and calculate the length of this path using the metric. You should find that the length of the path is actually 0, which on a 2D spatial manifold shows that these points with different coordinate representations are actually the same geometric point.

Defining what it means for points with different coordinate representations to "really" be the same geometric point in a spacetime manifold is a little trickier, because different points on the worldline of a light beam are genuinely different geometrically, and yet the integral of ds^2 along a light beam worldline is always zero. But I'm sure physicists do have some definition. One guess I had about this is that two different points in a coordinate system could be defined to be the same geometric point if it is impossible to find a purely spacelike or purely timelike curve with nonzero ds^2 going between them, such that the curve has no sharp "kinks" in it (if you allow sharp kinks, it would be possible to find a nonzero timelike worldline connecting a single geometric point to itself--just draw two different timelike worldlines emanating from that point, wordlines which cross at some other point, then define a new closed worldline that travels 'up' the first worldline until it reaches the crossing point, then travels back 'down' the second worldline until it returns to the original point).

edit: actually I realized my hypothesized definition doesn't work, because I don't think you can find a purely spacelike or timelike path of nonzero length to connect two points on the worldline of a light ray, at least not if you're considering paths in only one space dimension, and with more space dimensions you can easily find a spacelike path connecting a single geometric point to itself, just consider a loop that stays within a single plane of simultaneity. So my proposal was obviously on the wrong track, but like I said, I'm sure physicists have some definition.

Next, I have to question why its OK for a particle (or observer) to travel backwards in coordinate time as long as its/his/her proper time is advancing?

For any particle whatsoever, even one in flat SR spacetime, if you define the direction of increasing proper time along its worldline (which itself is a matter of convention rather than a physical fact, as I said earlier), you can always find some coordinate system where proper time is increasing as coordinate time is decreasing. Do you see this as less problematic because you somehow think Schwarzschild coordinates are privileged over any other arbitrary coordinate system? Only coordinate-independent geometric facts are really physical, I keep saying this and yet you seem to keep ignoring it.

I am very aware that my point of view is not the textbook point of view, but I am asking if there is the possibility of other equally valid physical interpretations of the equations of General Relativity?

No, I don't think any physicist would see any validity in an "interpretation" that converted GR into a non-geometric theory where some particular coordinate system was privileged over others. If you want to advance such a crazy notion you should go to the independent research forum, not here.

 

[Hurkyl]

Going back to my first question, I was informed (through a different channel) that the universal property of the maximally extended Schwarzschild solution is that it is the (real) analytic continuation of the external Schwarzschild chart.

If I recall the theory correctly, that means every analytic extension of the exterior Schwarzschild chart is, indeed, a quotient of a subspace of the maximally extended one.


Of course, this classification wouldn't apply to smooth extensions.

 

[DrGreg]

Removing the Schwarzschild coordinate singularity

kev, and those who have been responding to him, might like to use the new Removing the Schwarzschild coordinate singularity[/color] thread I have created, as a place to further discuss the issues raised without diverting from the main topic of this thread.