tomtomtom1
- 160
- 8
- Homework Statement
- Understanding Newton's 2nd Law of Motion
- Relevant Equations
- NA
Hello all
I am trying to understanding Newton's 2md Law of Motion which states:-
Force = Mass * Acceleration
If I had a force of 10Newtons pushing an object along the ground (assume no friction) in a perfectly horizontal direction that has a Mass of 10kg then the objects acceleration would be 5m/s^2 in the horizontal direction.
My question why is gravity factored into this as shown in my sketch below:-
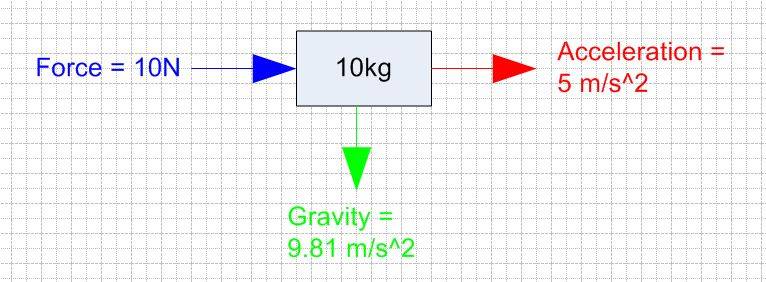
Gravity is acting on the mass while a force of 10N is being applied - so my question is shouldn't gravity be considered as another force acting downwards which would effect the acceleration and the direction of the Mass?
I hope this makes sense?
I am trying to understanding Newton's 2md Law of Motion which states:-
Force = Mass * Acceleration
If I had a force of 10Newtons pushing an object along the ground (assume no friction) in a perfectly horizontal direction that has a Mass of 10kg then the objects acceleration would be 5m/s^2 in the horizontal direction.
My question why is gravity factored into this as shown in my sketch below:-
Gravity is acting on the mass while a force of 10N is being applied - so my question is shouldn't gravity be considered as another force acting downwards which would effect the acceleration and the direction of the Mass?
I hope this makes sense?