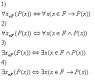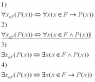Salt
- 15
- 0
I have no idea how to type math symbols into here so it's all in the PNG attached.
I'm probably kind of dumb for not getting this but...
I understand that 1) & 3) are true. And the 2) is not right, as it means all x are members of F and true for P(x) when we mean all x that are members of F are true for P(x).
But why do we use 3) instead of 4)?
I'm probably kind of dumb for not getting this but...
I understand that 1) & 3) are true. And the 2) is not right, as it means all x are members of F and true for P(x) when we mean all x that are members of F are true for P(x).
But why do we use 3) instead of 4)?