heartyface
- 28
- 0
*I am reposting as I previously posted this in the wrong category.
Perhaps I am confused by the concept.
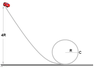
A toy car starts from rest at a height 4R above the ground and continue to a loop of radius R (frictionless). At a point C (height R from the ground) inside the loop, what is the tangential acceleration of the toy car?
I don't think a=alpha*r is quite relevant to this...or a=dv/dt...
not quite yet. perhaps the gravity is the only thing?
Please, explain me of the concept of 'tangential acceleration' and its components.
Homework Statement
Perhaps I am confused by the concept.
A toy car starts from rest at a height 4R above the ground and continue to a loop of radius R (frictionless). At a point C (height R from the ground) inside the loop, what is the tangential acceleration of the toy car?
Homework Equations
I don't think a=alpha*r is quite relevant to this...or a=dv/dt...
The Attempt at a Solution
not quite yet. perhaps the gravity is the only thing?
Please, explain me of the concept of 'tangential acceleration' and its components.