Understanding Valleys in the Conduction Band

[cr2504life]

Hi and thanks for reading,

I don't really understand the valleys in the conduction band, in the E vs. k diagram, there is the L-valley, r-valley and X-valley. Each has a different momentum... and are at different energy levels.

I understand that at any temperature above absolute zero, a small fraction of electrons will acquire enough energy to jump to the conduction band (overcome the energy gap Eg).

The GaAs bandstructure here:

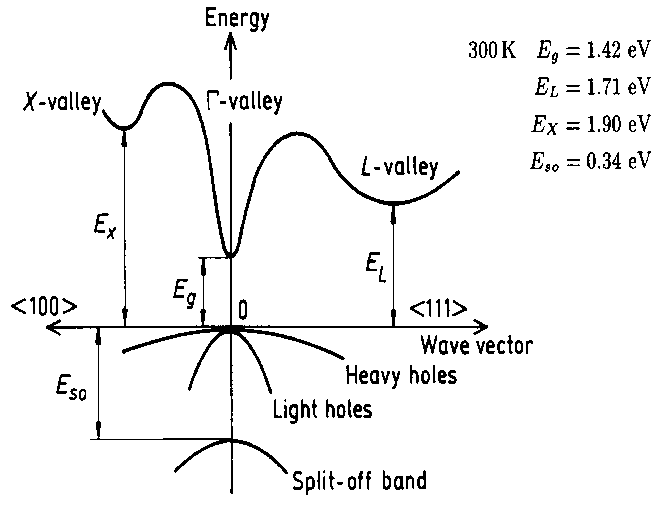
http://www.ioffe.ru/SVA/NSM/Semicond/GaAs/bandstr.html

I assume most electrons which acquire enough energy will jump to the lowest valley in the conduction band (r-valley for GaAs).

Ive been trying to determine what is the 'effective' temperature necessary to move an electron from the r-valley to the L-valley, the difference is 0.29 eV in GaAs.
Is the additional thermal energy comming from E = kT ?
... therefore T = 0.29eV*q/(k) ? this is a large temperature ... this seems too large ~3,600 °K.

How do the electons move between valleys ? And how does one find the required energy for this to take place ?
Thanks for any help you can provide.

 

[Kholdstare]

Although you can tell the required amount of energy an electron needs to jump from valance band top to the conduction band top, you cannot straightforward associate a temperature for this using E=kT. The electrons in a solid are distributed according to Fermi distribution function. And even in the room temperature (kT=0.026meV) a portion of the the Fermi function will reach conduction band. Hence quite handful of electrons will occupy above the conduction band.
http://en.wikipedia.org/wiki/Fermi–Dirac_statistics

 

[cr2504life]

I see from the solution now that the 'effective' temperature of an electron which moves from the r-valley to the L-valley is equal to T = 0.29eV*q/k ~ 3600 K, I had done this correctly.

 

[Dr Transport]

I see from the solution now that the 'effective' temperature of an electron which moves from the r-valley to the L-valley is equal to T = 0.29eV*q/k ~ 3600 K, I had done this correctly.

Math correct, physics wrong. Think about it, 3600 K, most likely GaAs is a vapour at that temperature, the melting point is 1240 C (1530 K). For an electron to move between the \Gamma-point and L-point of a lattice requires a phonon assist.