- #1
David112234
- 105
- 3
R
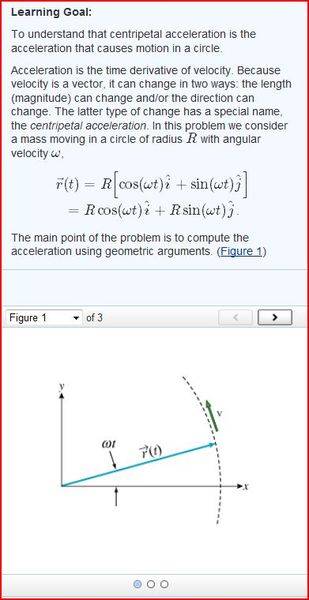
A
What is the velocity of the mass at a time t? You can work this out geometrically with the help of the hints, or by differentiating the expression for r⃗ (t) given in the introduction. (Figure 2)
Express this velocity in terms of R, ω, t, and the unit vectors i^ and j^.
B
Assume that the mass has been moving along its circular path for some time. You start timing its motion with a stopwatch when it crosses the positive x axis, an instant that corresponds to t=0. [Notice that when t=0, r⃗ (t=0)=Ri^.] For the remainder of this problem, assume that the time t is measured from the moment you start timing the motion. Then the time − t refers to the moment a time t before you start your stopwatch.
What is the velocity of the mass at a time − t?
Express this velocity in terms of R, ω, t, and the unit vectors i^ and j^.
C
What is the average acceleration of the mass during the time interval from − t to t? (Figure 3)
Express this acceleration in terms of R, ω, t, and the unit vectors i^ and j^.
2. Homework Equations
V=rω
a=rα
Rotational kinematics equations
For A:
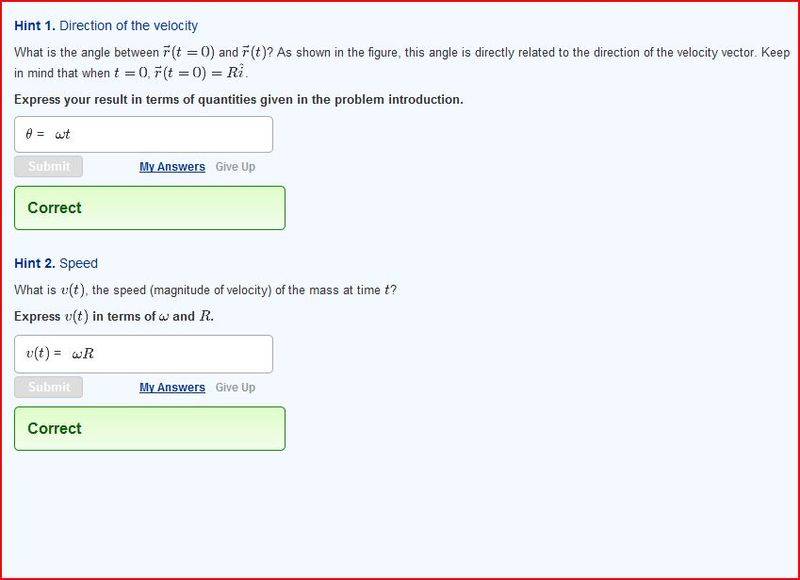
So from my understanding the radius will vary with time and ω but I do not see the relevance of that.
If V=rω
and the r given is R(cos(ωt){i}+sin(ωt){j}) then shouldn't the v be
R(cos(ωt){i}+sin(ωt){j}) * ω ?
I do not understand this question, what does differentiation have to do with this? That would just give me how it is changing, not v
Homework Statement
A
What is the velocity of the mass at a time t? You can work this out geometrically with the help of the hints, or by differentiating the expression for r⃗ (t) given in the introduction. (Figure 2)
Express this velocity in terms of R, ω, t, and the unit vectors i^ and j^.
B
Assume that the mass has been moving along its circular path for some time. You start timing its motion with a stopwatch when it crosses the positive x axis, an instant that corresponds to t=0. [Notice that when t=0, r⃗ (t=0)=Ri^.] For the remainder of this problem, assume that the time t is measured from the moment you start timing the motion. Then the time − t refers to the moment a time t before you start your stopwatch.
What is the velocity of the mass at a time − t?
Express this velocity in terms of R, ω, t, and the unit vectors i^ and j^.
C
What is the average acceleration of the mass during the time interval from − t to t? (Figure 3)
Express this acceleration in terms of R, ω, t, and the unit vectors i^ and j^.
2. Homework Equations
V=rω
a=rα
Rotational kinematics equations
The Attempt at a Solution
For A:
So from my understanding the radius will vary with time and ω but I do not see the relevance of that.
If V=rω
and the r given is R(cos(ωt){i}+sin(ωt){j}) then shouldn't the v be
R(cos(ωt){i}+sin(ωt){j}) * ω ?
I do not understand this question, what does differentiation have to do with this? That would just give me how it is changing, not v