Techsmart07
- 3
- 0
I have been taking an introduction to thermal/quantum physics course, and we are passing over quantum right now, and my teacher has us completely bewildered. This course is pre-differential equations, so most of the stuff is broadly explained, and the book has almost no examples for direction.
The figure below shows the wave function \Psi(x) for a particle confined between x=0 and x=L.A) Find an expression for A in order that the wave function can be normalized. B) What is the probability of finding the particle in the region 0<x<L/4?

2. relevant formulas
(sorry if its not perfect setup, not used to the math functions on here)
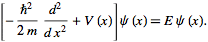
P(x) = \Psi2(x)dx
Honestly, I don't really even know what to do, so I couldn't make an attempt.
I feel lost on this entire section of the book...
Homework Statement
The figure below shows the wave function \Psi(x) for a particle confined between x=0 and x=L.A) Find an expression for A in order that the wave function can be normalized. B) What is the probability of finding the particle in the region 0<x<L/4?
2. relevant formulas
(sorry if its not perfect setup, not used to the math functions on here)
P(x) = \Psi2(x)dx
The Attempt at a Solution
Honestly, I don't really even know what to do, so I couldn't make an attempt.
I feel lost on this entire section of the book...