Unit vector in Magnetic boundary condition

[baby_1]

Hello
I'm getting confused when I want to use magnetic boundary equation

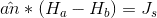
could you tell me how we define the unit vector(an) in this equation?
for example you assume that we have two different region (A in red and B in yellow) which vector (1,2,3,4) is right for

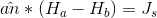equation and which is right for

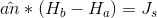too?

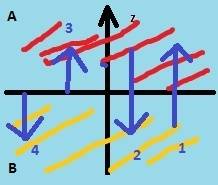
Thank you

 

[Simon Bridge]

Start by writing out the definition of $\hat a_n$ ... what does it represent?

 

[baby_1]

Thank you dear Simon
As I check the reference book an is a vector from region 2 to 1 according

equation it means an could be (az) and for

equation could be (-az) , Am I right?

 

[Simon Bridge]

No: axes are arbitrary so just relabelling it is begging the question.
You are having trouble like this because you are trying to do all your work in the tidy abstract world of pure algebra.
Science is messier than that.

Concentrate on the physical meaning of the unit vector you want to know about - there is something in the real physical world that it is supposed to represent and describe. What is it?

i.e. I may orient x-y-z axes so that the x-y plane lies on the surface of my window with y-axis pointing upwards.
Therefore - $\hat a_y$ is the unit vector pointing the opposite way to gravity, $\hat a_x$ is the unit vector pointing along the windowsill from left to right, and $\hat a_z$ is the unit vector pointing into the house and normal to the windowpane.

See what I mean? Each vector has a real-world meaning.
So what is the real-world meaning of $\hat a_n$?