Telemachus
- 820
- 30
Urgent! Thermodynamic refrigerator
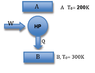
One mole of a monatomic ideal gas is allowed to expand isothermally from an initial volume of 10 liters to a final volume of 15 liters, the temperature being maintained at 400K. The work delivered is used to drive a thermodynamic refrigerator operating between reservoirs of temperatures 200 and 300K. What is the maximum of heat withdrawn from the low-temperature reservoir?
This is what I did:
u=cRT \rightarrow T=\frac{cR}{u}
Pv=RT \rightarrow P=\frac{RT}{v}
u=cRT=constant
du=\frac{u}{cR}ds-\frac{RT}{v}dv=0 \rightarrow \Delta s=r \ln\frac{v_f}{v_0}
Q_{12}=T \Delta S=400R \ln 1.5=-W_{12}
The thing is I'm having a negative work. I assume I'm making something wrong, I just can't see the mistake.
I have my exam tomorrow, so any help will be appreciated.
Homework Statement
One mole of a monatomic ideal gas is allowed to expand isothermally from an initial volume of 10 liters to a final volume of 15 liters, the temperature being maintained at 400K. The work delivered is used to drive a thermodynamic refrigerator operating between reservoirs of temperatures 200 and 300K. What is the maximum of heat withdrawn from the low-temperature reservoir?
This is what I did:
u=cRT \rightarrow T=\frac{cR}{u}
Pv=RT \rightarrow P=\frac{RT}{v}
u=cRT=constant
du=\frac{u}{cR}ds-\frac{RT}{v}dv=0 \rightarrow \Delta s=r \ln\frac{v_f}{v_0}
Q_{12}=T \Delta S=400R \ln 1.5=-W_{12}
The thing is I'm having a negative work. I assume I'm making something wrong, I just can't see the mistake.
I have my exam tomorrow, so any help will be appreciated.