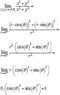Use polar coordinates to find the limit

Click For Summary

Homework Help Overview

The discussion revolves around using polar coordinates to evaluate a limit as the point approaches the origin in the Cartesian plane. The original poster presents an exercise that involves understanding the behavior of a function in polar coordinates.

Discussion Character

  • Exploratory, Conceptual clarification

Approaches and Questions Raised

  • Participants are discussing the steps taken so far and questioning how to determine the limit. There is a mention of the nature of continuous functions and their limits, prompting further inquiry into the original poster's understanding.

Discussion Status

The conversation is ongoing, with participants seeking clarification on the original poster's approach and exploring the concept of limits in the context of continuous functions. Some guidance has been offered regarding the nature of limits, but no consensus has been reached.

Contextual Notes

The original poster has not provided specific details about the function in question, which may affect the discussion. There is an emphasis on the transition to polar coordinates and the implications of approaching the origin.

Faka
Messages
25
Reaction score
0
Hi!
Is there somebody, who can help me with this exercise:
"Use polar coordinates to find the limit. [If (r, θ ) are polar coordinates of the point (x,y) with r ≥ 0, note that r --> 0+ as (x,y) --> (0,0)]
 

Attachments

  • Limit.jpg
    Limit.jpg
    2.6 KB · Views: 559
Physics news on Phys.org
What steps have you made so far?
 
I've done this so far. I do not know how to determine what the limit is.
 

Attachments

  • Limit 2.jpg
    Limit 2.jpg
    7.2 KB · Views: 981
Looks like a continuous function of r to be, what are the limits of continuous functions?
 
what do you mean exactly?
 
I hope this is right :smile:
 

Attachments

  • Limit 3.jpg
    Limit 3.jpg
    8.6 KB · Views: 1,256

Similar threads

Double Integral of function in region bounded by two circles
  • · Replies 19 ·
Replies
19
Views
3K
Trying to find this double integral using polar coordinates
  • · Replies 14 ·
Replies
14
Views
3K
Change of Variables: Integrals w/Polar Coordinates
  • · Replies 2 ·
Replies
2
Views
2K
Graphing Polar Coordinates: 0 ≤ θ ≤ π and 0 ≤ r ≤ 4
  • · Replies 2 ·
Replies
2
Views
2K
Integration of acceleration in polar coordinates
  • · Replies 24 ·
Replies
24
Views
4K
Triple Integral of y^2z^2 over a Paraboloid: Polar Coordinates Method
  • · Replies 6 ·
Replies
6
Views
2K
Show proof of point C in the given problem that involves Polar equation
  • · Replies 3 ·
Replies
3
Views
1K
Double Integration in Polar Coordinates
  • · Replies 3 ·
Replies
3
Views
2K
Double integral on triangle using polar coordinates
  • · Replies 3 ·
Replies
3
Views
3K
Trying to use polar coordinates to find the distance between two points
  • · Replies 7 ·
Replies
7
Views
2K