- #1
rwooduk
- 762
- 59
We have a waveform that is composed of several waves, maybe something like this:
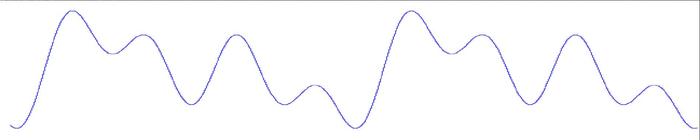
If we Fourier transform the graph we get something like this:
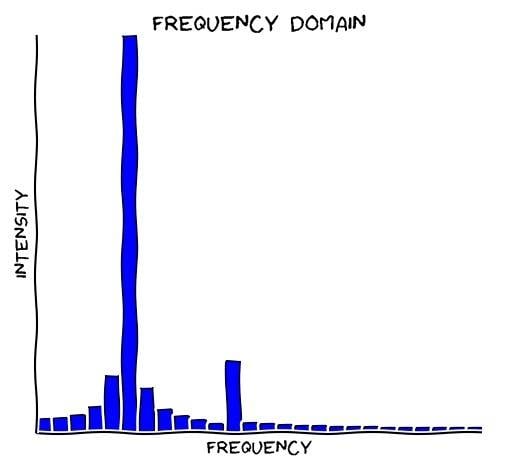
My question is, does the value of the largest column represent the peak to peak voltage of the waveform pictured above?
If we Fourier transform the graph we get something like this:
My question is, does the value of the largest column represent the peak to peak voltage of the waveform pictured above?