Using Z transforms to solve difference equations.

Uan · Oct 22, 2013

Hi,

We can use Laplace transforms to solve DEs with these guys:

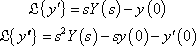
But what are the z transform versions in discrete time that include initial conditions, and how do you derive them? For example y[n+1], y[n+2] etc.

Thanks

Uan · Oct 22, 2013

As luck would have it after posting, found the answer here: https://www.physicsforums.com/showthread.php?t=493424

Time for a rest... :zzz:

Using Z transforms to solve difference equations.

Undergrad Why ##a^0=1##?

Undergrad Finding the minimum distance between two curves

Undergrad Mixed approximation vs. full approximation for a power series expansion

Undergrad Correct Upper/Lower limits for continuation of solutions for ODE

High School Arc Length for Hyperbolic Sin

Undergrad Correct Upper/Lower limits for continuation of solutions for ODE

Graduate About ellipticity and a proof that a system of PDEs is elliptic

Insights Revisiting the Velocity-Time Function

Insights Remote Operated Gate Control System

Insights AI Enriched Problem Solving

Insights Thinking Outside The Box Versus Knowing What’s In The Box

Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality

Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect

Using Z transforms to solve difference equations.

Similar threads