Utilizing Cayley-Hamilton's Theorem to Solve N x N Determinant Problem

[kockabogyo]

1. Given A,B\in Mat _n(\mathbb{R})

2. Show that:
a) \det (A^2 + A + E)\geq 0
b) \det (E+A+B+A^2+B^2)\geq 0 ,
where E is the unit matrix.3. My attempt at a solution
A^2 + A + E=(A + E)^2 -2A

https://drive.google.com/file/d/0B8zKPTh1siSsOHNWQnBfaXR3QXM/view?usp=sharing

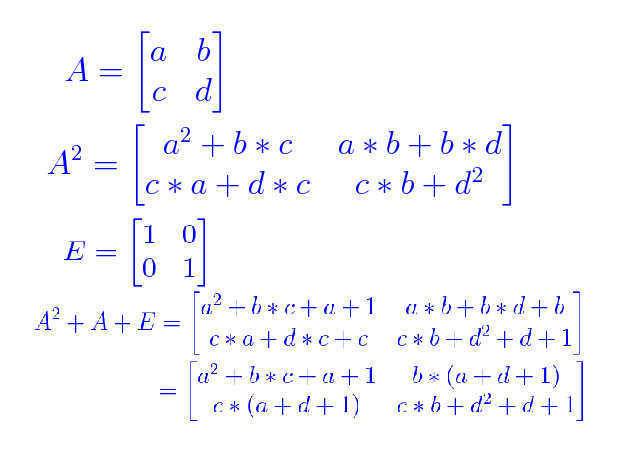
pleas give me tips to solve

 

[mfb]

A^2 + A + E=(A + E)^2 -2A

Something went wrong with the linear term, and I would choose a different term to square.

You can consider the cases $det(A)=0$ and $det(A) \neq 0$ separately, that gives more freedom to manipulate A in one case.

 

[kockabogyo]

Something went wrong with the linear term, and I would choose a different term to square.

You can consider the cases $det(A)=0$ and $det(A) \neq 0$ separately, that gives more freedom to manipulate A in one case.

Thanks, yes, sorry not - 2A only -A , but than?

 

[mfb]

I would choose a different term to square. A term that doesn't leave an A outside.

 

[kockabogyo]

I would choose a different term to square. A term that doesn't leave an A outside.

O Yeah!.. I think I found it.. Cayley Hamilton's context A² - Tr(A)*A+det(A)*E = O