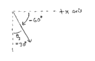Vector addition- Positive x axis.

In summary, Vector addition on the positive x-axis is the process of combining two or more vectors that are aligned in the same direction along the x-axis. This results in a new vector with a magnitude equal to the sum of the individual vectors' magnitudes, and a direction that is the same as the original vectors. To perform vector addition on the positive x-axis, you must first determine the magnitude and direction of each vector. Then, align the vectors so that they are all pointing in the same direction along the x-axis. Finally, add the magnitudes of each vector to get the magnitude of the resultant vector. Vector addition on the positive x-axis involves adding vectors with both magnitude and direction, while scalar addition only involves adding the magnitudes of
  • #1
opus
Gold Member
717
131
Please see the attached page to see what I'm talking about.
In the top right paragraph, it states to use "the positive direction of the x-axis".
It is given that ##θ_2=30°## and it shown visually at the bottom of the page.
In the problem it's using -60° and I'm not sure how they're getting that.
 
Mathematics news on Phys.org
  • #2
Given pictures
 

Attachments

  • C8AF2925-DF43-4D00-93CC-CA8323054359.jpeg
    C8AF2925-DF43-4D00-93CC-CA8323054359.jpeg
    40.9 KB · Views: 376
  • #3
Here's the second vector by itself. Counterclockwise from the +x axis is a positive angle; clockwise from the +x axis is negative.

angle.gif
 

Attachments

  • angle.gif
    angle.gif
    5.3 KB · Views: 563
  • Like
Likes opus
  • #4
Exactly what I was looking for. Thank you @jtbell.
 

FAQ: Vector addition- Positive x axis.

1. What is vector addition?

Vector addition is the process of combining two or more vectors to create a new vector. It involves adding the corresponding components of the vectors together to determine the magnitude and direction of the resulting vector.

2. What is the positive x axis in vector addition?

The positive x axis is a reference line used in vector addition to represent the horizontal direction. It is usually drawn as a straight line pointing to the right, with the origin (0,0) at the left end.

3. How is vector addition performed on the positive x axis?

In vector addition on the positive x axis, the magnitudes of the vectors are added together while taking into account their direction. If the vectors are in the same direction, their magnitudes are simply added. If they are in opposite directions, the magnitude of the smaller vector is subtracted from the magnitude of the larger vector.

4. What is the result of vector addition on the positive x axis?

The result of vector addition on the positive x axis is a single vector with a magnitude and direction that represents the combined effect of the individual vectors. This resulting vector can be graphically represented as an arrow pointing in the direction of the positive x axis with a length equal to the magnitude of the resulting vector.

5. What are some real-life applications of vector addition on the positive x axis?

Vector addition on the positive x axis is used in various fields such as physics, engineering, and navigation. For example, it can be used to calculate the net force acting on an object in physics, determine the resultant force on a structure in engineering, or calculate the displacement of a ship in navigation.

Similar threads

B Multiple Rotating Signs on a Fence Gate -- Overlap Question
Replies
4
Views
821
B Notation for a "scalar absolute field"?
Replies
1
Views
922
MHB Left or Right Angles ( + or - ) of adjoining vectors
Replies
2
Views
1K
I What is the role of geometry and dimensional operations?
Replies
3
Views
1K
B A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
Replies
13
Views
2K
B Heard of Another Kind of "Rational" (Fraction) Addition?
Replies
8
Views
1K
Question about magnitude positive y direction
Replies
2
Views
991
MHB Angle calculation in a sloping vector system
Replies
1
Views
1K
MHB Calculating the Angle between Ship and Rock
Replies
18
Views
4K
Vector is a function of its position or not?
Replies
16
Views
974

Hot Threads

Recent Insights

Back
Top