- #1
arkajad
- 1,481
- 4
I am reading the Wikipedia entry http://en.wikipedia.org/wiki/Vector_fields_in_cylindrical_and_spherical_coordinates" . There, in particular I see this:
So, I wonder, what is the rationale behind assuming that x,y,z are time-independent but [tex]\rho, \theta,\phi[/tex] suddenly depend on time even if the realtions between the two are time-independent? Can someone help me here?
Time derivative of a vector field
To find out how the vector field A changes in time we calculate the time derivatives. In cartesian coordinates this is simply:
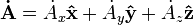
However, in spherical coordinates this becomes:
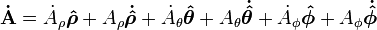
To find out how the vector field A changes in time we calculate the time derivatives. In cartesian coordinates this is simply:
However, in spherical coordinates this becomes:
So, I wonder, what is the rationale behind assuming that x,y,z are time-independent but [tex]\rho, \theta,\phi[/tex] suddenly depend on time even if the realtions between the two are time-independent? Can someone help me here?
Last edited by a moderator: