Discussion Overview
The discussion revolves around the effect of a pulley on the free body diagram of a beam subjected to a load. Participants explore the implications of introducing a pulley system in terms of axial loads, tension forces, and equilibrium conditions, focusing on both theoretical and practical aspects of statics.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
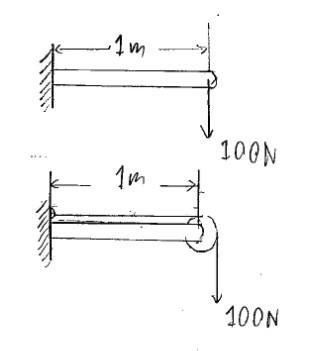
- One participant presents a scenario involving a 1-m bar fixed to a wall with a 100 N weight, questioning how the free body diagram changes with the addition of a pulley.
- Another participant mentions axial load in the beam under compression but does not elaborate on its implications.
- There is a request for clarification on the magnitude of the axial force in the beam and the reasoning behind it, emphasizing the use of free body diagrams and equilibrium equations.
- A participant explains that the tension in a rope through an ideal pulley is equal on both sides, suggesting that the force exerted by the wall on the rope must equal the tension, affecting the forces acting on the beam.
- It is proposed that drawing a free body diagram of the pulley can help identify the direction of tension forces, leading to the conclusion that the beam experiences the same horizontal and vertical forces, but with an additional axial force that remains unspecified.
Areas of Agreement / Disagreement
Participants express differing views on the specifics of the axial force and its calculation, indicating that the discussion remains unresolved regarding the exact magnitude and implications of the forces involved.
Contextual Notes
Participants have not reached a consensus on the magnitude of the axial force in the beam, and there are unresolved aspects regarding the assumptions made in the free body diagrams and equilibrium equations.