bergausstein
- 191
- 0
Another Venn diagram problem. just want to check if my answer is correct since i don't have a solutions manual of the book I'm using.
Use Venn diagrams to illustrate the following.
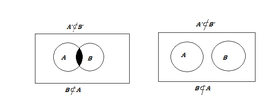
a. $\displaystyle A\cup B\,=\,A$ if and only if $\displaystyle B\subset A$
b. $\displaystyle A\cap B\,=\,B$ if and only if $\displaystyle B\subset A$
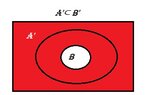
c. $\displaystyle B\subset A$ if and only if $\displaystyle A'\subset B'$
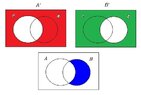
d. $\displaystyle \left(A'\right)'\,=\,A$
my answers
View attachment 1110
Use Venn diagrams to illustrate the following.
a. $\displaystyle A\cup B\,=\,A$ if and only if $\displaystyle B\subset A$
b. $\displaystyle A\cap B\,=\,B$ if and only if $\displaystyle B\subset A$
c. $\displaystyle B\subset A$ if and only if $\displaystyle A'\subset B'$
d. $\displaystyle \left(A'\right)'\,=\,A$
my answers
View attachment 1110