Very basic fluid statics and dynamics question

[iScience]

consider the image on the drawing at the top (above the yellow arrow)

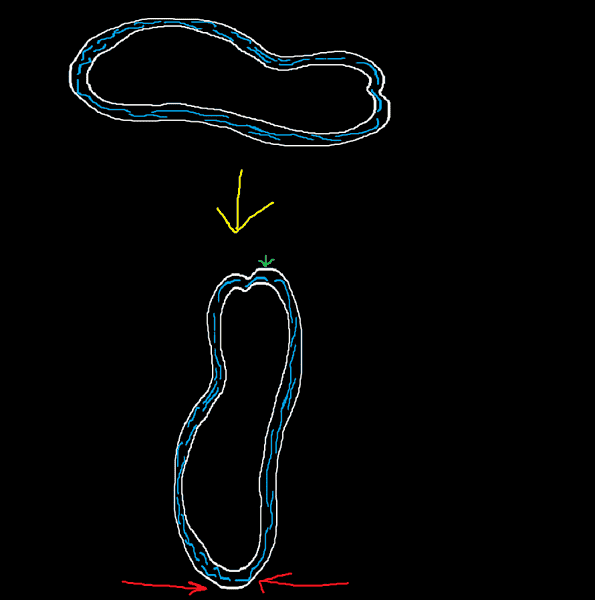
if i had some non-compressible fluid enclosed in a pipe like container that looped back in on itself (as shown in figure), and if the container was non-elastic, when i rotate this container filled with fluid such that the long axis is vertical, i suspect, that for a short lived time interval, that there will initially be greater pressure at the bottom (where the red arrows are), and there will be a negative pressure at the very top (green arrow). However, because the fluid is incompressible, and encased in a closed container (there is no air inside the container), i suspect that any pressure gradients in the fluid will quickly equilibrate with the rest of the system (fluid). so, my question is, when i rotate the container such that its long axis is vertical, will i get an increase in pressure in my system? or will the pressure gradients cancel exactly?

 

[olivermsun]

So imagine if you just had a single tube (assume the fluid can flow in a circle if it wants to), and repeat the thought experiment. What would you expect to happen to the pressure measured at various places in the tube?

What if you keep the rotation going?

 

[iScience]

single tube? are you referring to a straight flat tube with an inlet on one end and an outlet on the other?

 

[Chestermiller]

The pressure will be higher at the bottom of the container and lower at the top of the container because of the hydrostatic head of liquid. This will not go away with time.

If the fluid is perfectly incompressible, then the absolute values of the pressures are indeterminate. You know this because, if you change the pressure on an incompressible fluid, the volume doesn't change. So if you did this experiment with two different starting pressures in the fluid, you would get the same result.

The only way to get the absolute values of the pressures is to treat the fluid as compressible, and to specify the initial pressure before the loop is rotated into the new position.

Chet

 

[PJC01]

I can confirm that your suspicion is correct. When the container is rotated, there will initially be a difference in pressure at the bottom and top due to the gravitational force acting on the fluid. However, since the fluid is incompressible and the container is closed, the pressure gradients will quickly equilibrate and there will be no net increase in pressure in the system. This is because the fluid will redistribute itself in response to the change in orientation, resulting in the cancellation of any pressure gradients. This phenomenon is known as hydrostatic equilibrium and is a fundamental principle in fluid statics.