Danyon
- 83
- 1
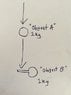
Consider two objects, "A" and "B", each having mass 1kg. Object "A" moves downward towards object "B" and collides with the extended arm of object "B". Let's say for the sake of argument that during this collision object "A" lost one unit of momentum and 0.5 joules to object "B" (This value does not matter because the thought experiment works for all possible values). If conservation of linear momentum applies then object "B" should then begin to move downwards with momentum 1 and energy 0.5, the movement downwards has used all the available energy (0.5 joules) However, because object "A" struck object "B" off center, object "B" should begin rotating, this should give the object an additional rotational energy, violating the law of conservation of energy. If energy is conserved in this system then the energy of the rotation must be stolen from the energy associated with the downward movement, which would violate conservation of linear momentum. Any thoughts?