SUMMARY
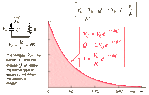
The discussion focuses on the behavior of two capacitors, specifically 10µF and 20µF, connected in series and charged with a 100V battery. After disconnecting from the battery and connecting to a 2500Ω resistor, the voltage across the capacitors after 1 second is determined using the formula V_C = V_0 e^(-t/RC). The combined capacitance for capacitors in series is calculated using the formula 1/(1/C1 + 1/C2). The exponential decay of voltage is emphasized, highlighting the importance of the negative sign in the discharge formula.
PREREQUISITES
- Understanding of capacitor charging and discharging principles
- Familiarity with the formula for combined capacitance in series
- Knowledge of exponential decay functions
- Basic circuit analysis involving resistors and capacitors
NEXT STEPS
- Study the derivation of the capacitor discharge formula V_C = V_0 e^(-t/RC)
- Learn about RC time constant and its significance in circuit design
- Explore practical applications of capacitors in timing circuits
- Investigate the effects of different resistor values on capacitor discharge rates
USEFUL FOR
Electrical engineers, physics students, and hobbyists interested in circuit design and analysis, particularly those focusing on capacitor behavior in RC circuits.