- #1
gloo
- 261
- 2
I am looking at all these speed and acceleration equations on the net but can't find what I need. What I want to calculate is how far do i have to drop water for it to reach a certain speed?
The only equations i see involve asking parameters that I don't know. the only thing i do know is acceleration (9.81m/s square), and initial velocity which is zero. I am looking at final velocity equation Vfinal=Vinitial + a*t
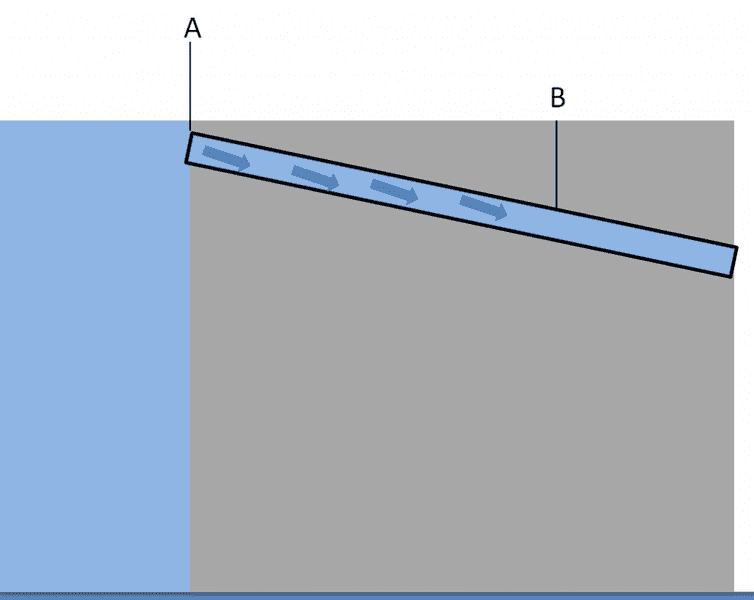
I have attached a diagram of what I am looking at. So at point A, the velocity is 0 (we are holding back water). If I want to achieve say 10meters per second at point B, I assume it has to drop a certain distance vertically??
How do solve for something like that final speed ...If i want to achieve say 10 m/s final velocity?
The only equations i see involve asking parameters that I don't know. the only thing i do know is acceleration (9.81m/s square), and initial velocity which is zero. I am looking at final velocity equation Vfinal=Vinitial + a*t
I have attached a diagram of what I am looking at. So at point A, the velocity is 0 (we are holding back water). If I want to achieve say 10meters per second at point B, I assume it has to drop a certain distance vertically??
How do solve for something like that final speed ...If i want to achieve say 10 m/s final velocity?