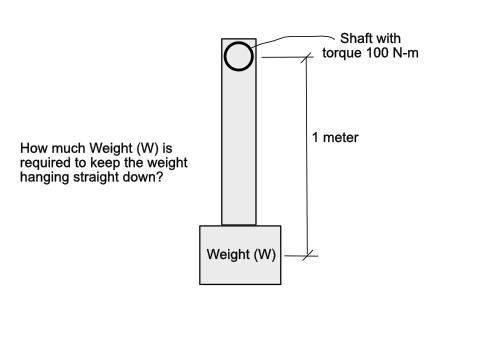
SUMMARY
The discussion focuses on calculating the weight (W) required to maintain a weight hanging straight down when torque is known on a rotating shaft. The key formula presented is the torque of weight around the central point of the shaft, expressed as T_W = W · 1m · sin(0), which results in zero torque for any finite W. The conversation also touches on the implications of infinite weight, suggesting that if W approaches infinity, the torque may stabilize the system, preventing rotation. The discussion highlights the complexities of torque calculations in mechanical systems.
PREREQUISITES
- Understanding of torque and its calculation in mechanical systems
- Familiarity with basic physics concepts, particularly gravity's effect on weight
- Knowledge of rotational dynamics and equilibrium conditions
- Experience with mathematical modeling in physics
NEXT STEPS
- Study the principles of torque in rotating systems using "Engineering Mechanics: Dynamics" by J.L. Meriam
- Explore the concept of equilibrium in mechanical systems through "Mechanics of Materials" by Ferdinand P. Beer
- Learn about the effects of infinite weight in theoretical physics contexts
- Investigate the implications of macro scale accelerations in mechanical modeling
USEFUL FOR
This discussion is beneficial for mechanical engineers, physics students, and anyone involved in the design and analysis of rotating systems and torque applications.