Weinberg gives relations of SO(3)

[kent davidge]

(Weinberg QFT, Vol 1, page 68)

He considers Mass-Positive-Definite, in which case the Little Group is SO(3). He then gives the relations

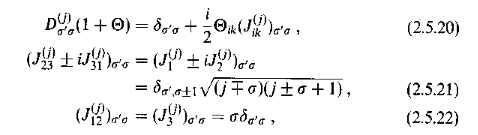
Is it difficult to derive these relations? I'm asking this mainly because I haven't seen them anywhere other than in Weinberg's book.

Also, I'm finding them difficult to follow, as on one side of the equations the $J$ have two indices whereas on the other side they have only one index.

 

[strangerep]

These are just some standard relations used when dealing with SO(3), but (as usual) Weinberg's treatment/notation makes it seem more difficult that it really is. Generally, Weinberg is able to deepen an existing understanding, but is not good for learning things the first time.

If you haven't already studied angular momentum aspects of ordinary QM, then try Ballentine ch7. In particular, in sect 7.1 Ballentine derives the quantum spectrum applicable to angular momentum (corresponding to the little $j$'s and $\sigma$'s). Where Weinberg uses $\sigma$'s, Ballentine uses the (more common?) symbol $m$.

After you've studied the material in Ballentine, you should be able to relate it back to Weinberg's formulas more easily.

 

[king vitamin]

Also, I'm finding them difficult to follow, as on one side of the equations the JJJ have two indices whereas on the other side they have only one index.

This is the standard notation in three dimensions. In D spatial dimensions, there are D(D-1)/2 independent rotations, and they are usually arranged in an antisymmetric tensor J_{ij} = -J_{ji} where i and j run from 1 to D. In three dimensions, it is conventional to define an angular momentum pseudovector J_i \equiv \epsilon_{ijk} J_{jk}, which extracts the three independent components of this tensor. The latter is the angular momentum vector you've encountered throughout physics, but it's important to keep in mind that angular momentum cannot be expressed as a vector in other dimensionalities.

 

[kent davidge]

try Ballentine ch7. In particular, in sect 7.1 Ballentine derives the quantum spectrum applicable to angular momentum

Hey, is what Ballentine does the same or similar as what's in http://www.cmth.ph.ic.ac.uk/people/d.vvedensky/groups/Chapter8.pdf ?

I'm asking this because if it's the same derivation, I'll be done with that one, because it's quite difficult for me to get Ballentine's book in my hands.

 

[strangerep]

Hey, is what Ballentine does the same or similar as what's in http://www.cmth.ph.ic.ac.uk/people/d.vvedensky/groups/Chapter8.pdf ?

That's excruciatingly tedious compared to Ballentine's more direct physicist-oriented treatment.

[...] it's quite difficult for me to get Ballentine's book in my hands.

See your private conversations page.