Weird relation: its graph is the formula

[phoenixthoth]

I thought this was really odd. I wonder if they found it by accident or were trying to do this...

http://mathworld.wolfram.com/TuppersSelf-ReferentialFormula.html

Apparently, the graph of this formula is the formula:

graph of formula:

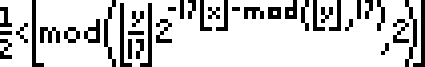
the formula:
http://mathworld.wolfram.com/images/equations/TuppersSelf-ReferentialFormula/equation1.gif

 

[ice109]

that's ridiculous

 

[phoenixthoth]

i know!

how could they say the graph of the formula is the formula when the two m's in the graph don't even look exactly the same?

http://mathworld.wolfram.com/images/gifs/TuppersFormula.gif

 

[HallsofIvy]

A "graph" is a set of points. A "formula" is a set or symbols. What, exactly, do you mean by "the graph of the formula is the formula"?

 

[phoenixthoth]

A "graph" is a set of points. A "formula" is a set or symbols. What, exactly, do you mean by "the graph of the formula is the formula"?

I mean that the picture of the graph

http://mathworld.wolfram.com/images/gifs/TuppersFormula.gif

is the formula that generated it

http://mathworld.wolfram.com/images/equations/TuppersSelf-ReferentialFormula/equation1.gif

 

[HallsofIvy]

And I will assert again that a picture is not a formula!
What exactly do you mean?

 

[ice109]

aww comon halls you're being to picky. the graph of the formula/equation/algorithm draws out the formula/equation/algorithm

whatever amorphous concept we are witness to by looking at that picture and reading the wolfram blurb, it's cool.

 

[phoenixthoth]

I still mean that the picture of the graph

http://mathworld.wolfram.com/images/gifs/TuppersFormula.gif

is the formula that generated it

http://mathworld.wolfram.com/images/equations/TuppersSelf-ReferentialFormula/equation1.gif

So when you say that a picture isn't a formula, that means you don't consider the following picture to be that of a formula?
http://tbn0.google.com/images?q=tbn:o76vMDPlG64nxM:http://www.atlanticwinds.com/mathmem/quadratic_formula.gif
After all, if formulas are just collections of symbols, do you think that pictures can't contain symbols?

 

[phoenixthoth]

aww comon halls you're being to picky. the graph of the formula/equation/algorithm draws out the formula/equation/algorithm

whatever amorphous concept we are witness to by looking at that picture and reading the wolfram blurb, it's cool.

Seems like HOI would say that the graph of y=3x+2 is NOT a line because its graph is actually a set of points. In fact, y=3x+2 isn't even a formula because it's not a set of symbols: {y=3x+2} is a formula while y=3x+2 is not.

It's called abuse of language and it happens all the time.

 

[christianjb]

Anyone for Goedel?

 

[HallsofIvy]

Seems like HOI would say that the graph of y=3x+2 is NOT a line because its graph is actually a set of points. In fact, y=3x+2 isn't even a formula because it's not a set of symbols: {y=3x+2} is a formula while y=3x+2 is not.

It's called abuse of language and it happens all the time.

No, I would definitely say that the graph of y= 3x+ 2 is a line. I would object to saying that "3x+ 2 is a line"!

Saying that {y= 3x+2} is a formula because it is a set of symbols while "y= 3x+ 2" is not- not that's picky!

 

[phoenixthoth]

Ok, so the graph of y=3x+2 is a line because if you draw a picture of the graph, the result looks like a line. Similarly, if you draw a picture of the graph of the formula http://mathworld.wolfram.com/images/equations/TuppersSelf-ReferentialFormula/equation1.gif
the result looks like the formula that the graph is generated by.

 

[christianjb]

Since all formulae on these web-pages are composed of pixels- I would definitely have to allow that a picture of a formula is a formula itself.

 

[phoenixthoth]

do yall think they found this by accident or were looking for this for some strange reason?

 

[Gib Z]

It definitely wasn't found by accident. How they did it though, I can't tell you, or else I'd have to kill you =]

 

[christianjb]

I followed the link on the mathworld page to the entry on self recursion. It's got a good puzzle:

What is the volume of a pizza of thickness a and radius z?

 

[HallsofIvy]

I followed the link on the mathworld page to the entry on self recursion. It's got a good puzzle:

What is the volume of a pizza of thickness a and radius z?

It took me a moment- I'm kinda slow- but yes, that is good.

 

[HallsofIvy]

Okay, I finally broke down and looked at all the references- Yes, its weird and I must agree that in this case the graph is the formula!

 

[uart]

do yall think they found this by accident or were looking for this for some strange reason?

No phoenixthoth, the formula is interesting but not nearly as weird or mysterious as you may first think. I have to admit when I first saw it today I was pretty "blown away", until I figured out how it works. It's actually nothing more than a recipe for decoding an arbitrary binary bitmap (monochrome, height=17, width=arbitrary). The bitmap is stored in the huge number n. Imagine each vertical column of dots in the bitmap being represented by a 17 digit binary number. Now imagine all of those 17 bit numbers being concatanated into one large binary number. Well that's what "n" is.

Look closly at the formula. First notice that the whole LHS expression is modulo 2. That just decodes each binary bit to either a "0" ot a "1" (0 if the inequality is false, 1 if it is true). Now look at the 2^(-17 floor(x) ...) part of the expression. Can you see that this is merely shifting the bits in the binary number. The mod(floor(y),17) part is shifting out the bits in each column (that is, as y is varied for a given x) while the 17 floor(x) part is shifting the bits 17 at a time (that is, selecting a different 17 bit column bitmap for each different value of x).

You see it's actually fairly straight forward once you see how it works. The formula can "draw" any bit map that you can make with a height of 17 pixels and arbitrary width, all by constructing the appropriate number "n".

 

[phoenixthoth]

Okay, I finally broke down and looked at all the references- Yes, its weird and I must agree that in this case the graph is the formula!

It would have been easier on me if PF allowed img tags to produce images... Then you wouldn't have had to go through the trouble of clicking a couple links.

uart: interesting analysis. thanks.

pizza! um, yeah...

 

[Gib Z]

No phoenixthoth, the formula is interesting but not nearly as weird or mysterious as you may first think. I have to admit when I first saw it today I was pretty "blown away", until I figured out how it works. It's actually nothing more than a recipe for decoding an arbitrary binary bitmap (monochrome, height=17, width=arbitrary). The bitmap is stored in the huge number n. Imagine each vertical column of dots in the bitmap being represented by a 17 digit binary number. Now imagine all of those 17 bit numbers being concatanated into one large binary number. Well that's what "n" is.

Look closly at the formula. First notice that the whole LHS expression is modulo 2. That just decodes each binary bit to either a "0" ot a "1" (0 if the inequality is false, 1 if it is true). Now look at the 2^(-17 floor(x) ...) part of the expression. Can you see that this is merely shifting the bits in the binary number. The mod(floor(y),17) part is shifting out the bits in each column (that is, as y is varied for a given x) while the 17 floor(x) part is shifting the bits 17 at a time (that is, selecting a different 17 bit column bitmap for each different value of x).

You see it's actually fairly straight forward once you see how it works. The formula can "draw" any bit map that you can make with a height of 17 pixels and arbitrary width, all by constructing the appropriate number "n".

You are my Hero :) I'm going to try make one that spells out some vulgar words :P

 

[matticus]

i thought that was the coolest thing i'd ever seen ever until i realized that it was not a miracle but rather a necessity that there was a value of n that drew the formula.

a little disappointing...

 

[matticus]

this is for n = 22701801293785014193580405120204586741061235962766583907094021879215171483119139894870133091111044901683400949483846818299518041763507948922590774925466088171879259465921026597046700449819899096862039460017743094473811056991294128542891880855362707407670722593737772666973440977361243336397308051763091506836310795312607239520365290032105848839507981452307299417185715796297454995023505316040919859193718023307414880446217922800831766040938656344571034778553457121080530736394535923932651866030515041060966437313323672831539323500067937107541955437362433248361242525945868802353916766181532375855504886901432221349733

 

[mongoose]

haha...that's sweet!