john321654
- 1
- 0
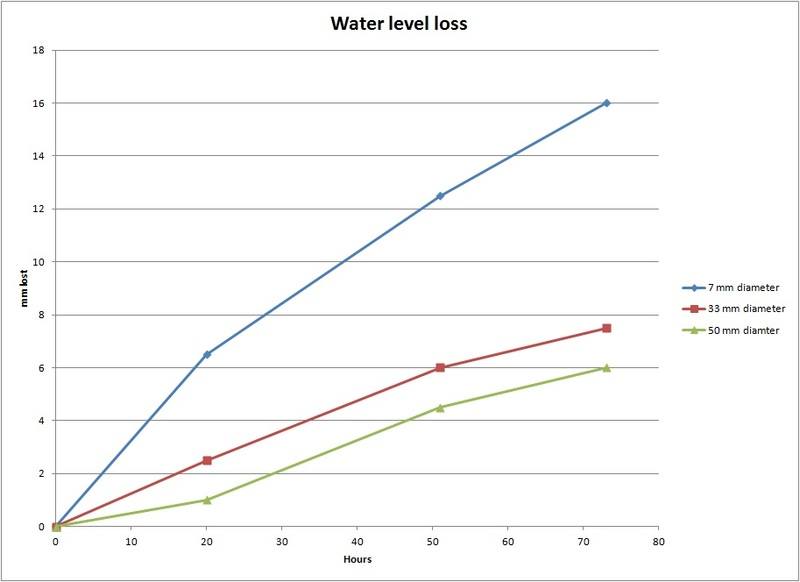
I am doing a senior design project regarding water hydration and did some tests to get a general evaporation rate. I assumed that evaporation is proportional to the surface area of the water to air boundary so I thought that the water level of water in any constant cross section container should fall at the same rate. However, upon testing different sized plastic containers all next to each other, I found that the water level fell much faster in my 7 mm diameter plastic tube than in the 33 mm or 50 mm diameter tubes over several days. All the containers started filled to the brim and had a box covering them to stop light and any air currents.
My question is that why would the water level drop much faster in the smaller diameter tube?
Could it have something to do with the volume of water, the surface area of the container to the volume of water, the meniscus, or capillary action?
Here's a graph of the data.
My question is that why would the water level drop much faster in the smaller diameter tube?
Could it have something to do with the volume of water, the surface area of the container to the volume of water, the meniscus, or capillary action?
Here's a graph of the data.