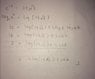lurflurf
Homework Helper
- 2,459
- 159
That attachment is fine.MissP.25_5 said:Since the instruction says to find all solutions, doesn't that mean ln have to be multivalued? Multivalued means k>0, right? k=0 would be the principle value, which is single valued, isn't it?
Can you check the attachment?
It is a minor technicality. To find all solutions we can use a multivalued inverse, or we can use a single value inverse to generate all solutions. k=0 can be the principal value if it is set up that way
your last post is confusing
where did i^0 come from?
third line from the bottom should have 2k pi i
then it should in the next line become 2k pi when you multiply both sides by -i