- #1
STINGERX
- 10
- 0
i found that in Anechoic chamber there are pyramidal structures over the walls,
what are the geometries of the height and base of those pyramids?
W and H on the picture:
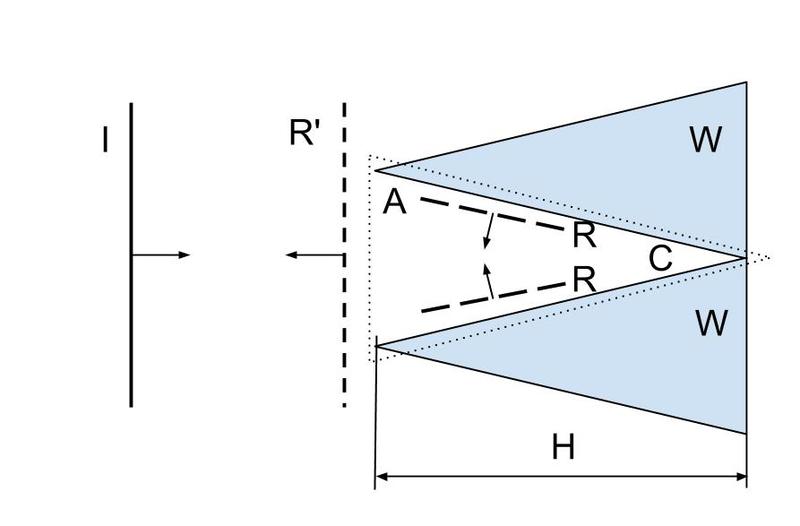
what are the geometries of the height and base of those pyramids?
W and H on the picture: