Bensky
- 82
- 0
Electric force angles problem :(
Three positive particles of charges 11.0 µC are located at the corners of an equilateral triangle of side d = 14.0 cm (Fig. 16-38). Calculate the magnitude and direction of the net force on each particle.
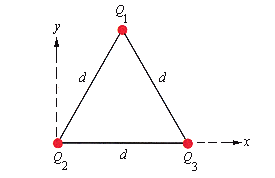
Fig. 16-38
F = KQ_1Q_2/r^2
F = KQ_1Q_2/r^2
F = (9X10^9)(1.1X10^-5)^2/.14^2
F = 55.561 N for all points - Q1, Q2, and Q3 (correct)
Q1 angle = 90 degrees (correct)
Q2 angle = ?
Q3 angle = ?
I need to find the directional angle for particles Q2 and Q3 - I am unsure how to find these. I was thinking I might have to draw a triangle?
Thanks,
Bensky
Homework Statement
Three positive particles of charges 11.0 µC are located at the corners of an equilateral triangle of side d = 14.0 cm (Fig. 16-38). Calculate the magnitude and direction of the net force on each particle.
Fig. 16-38
Homework Equations
F = KQ_1Q_2/r^2
The Attempt at a Solution
F = KQ_1Q_2/r^2
F = (9X10^9)(1.1X10^-5)^2/.14^2
F = 55.561 N for all points - Q1, Q2, and Q3 (correct)
Q1 angle = 90 degrees (correct)
Q2 angle = ?
Q3 angle = ?
I need to find the directional angle for particles Q2 and Q3 - I am unsure how to find these. I was thinking I might have to draw a triangle?
Thanks,
Bensky