zorro
- 1,378
- 0
Homework Statement
The Attempt at a Solution
Is there any difference between the above expression and
Is there any relation between these two?
Abdul Quadeer said:Homework Statement
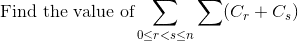
VietDao29 said:Are you sure there are up to 2 sigma signs in that expression?
tiny-tim said:can you find an exact equation for the difference between the second and twice the first?