What are the stresses at point A in a combined loading problem?

[Double A]

Homework Statement

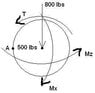
See attachment.

Homework Equations

A = \pi r^2

I_x = I_z = \frac{\pi}{4}r^4

J = \frac{\pi}{2}r^4 = 2I_x

Q = \Sigma A_i y_i

\sigma_{Axial} = \frac{P}{A}

\sigma_{Bending} = \frac{Mc}{I}

\tau_{Shear} = \frac{VQ}{Tt}

\tau_{Torque} = \frac{Tr}{J}

The Attempt at a Solution

I moved the applied forces to the location at point A with the corresponding moments and torques caused by the applied loads giving me the following values:

A = \pi(0.75in)^2 = 1.77 in^2

I_x = I_z = \frac{\pi}{4}(0.75 in)^4 = 0.249 in^4

J = 2(0.249 in^4) = 0.497 in^4

M_x = (800lbs)(10in) = 8 kips-in

M_y = T = (800lbs)(14in) = 11.2 kips-in

M_z = (500lbs)(14in) = 7 kips-in

\sigma_{Axial} = \frac{500 lbs}{1.77 in^2} = 282.9 psi

\sigma_{Bending} = \frac{(7 kips-in)(0.75 in)}{0.249 in^4} = 21.1 ksi

\tau_{Torque} = \frac{(11.2 kips-in)(0.75 in)}{0.497 in^4} = 16.9 ksi

Now I am not sure if the shear force has an affect on point A. If it does then how would you go about finding Q? I know that point A is on the x-axis and at the left edge of the rod. At this point I think the shear force does not cause a shear stress. Also the moment produced around the x-axis does not cause a normal stress because point A is on the centroid for the x-axis.

Now assuming what I have stated above is true then the only stresses acting at A are normal stresses in the y-direction and shear stresses in the y-z plane.

So then,

\sigma_y = \sigma_{Axial} + \sigma_{Bending} = 282.9 psi + 21.1 ksi = 21.4 ksi

\tau_{yz} = \tau_{Torque} = 16.9 ksi

So I guess what I want to know is does the shear force cause a shear stress and am I also accounting for all the elements that cause a normal stress or shear stress at point A?

 

[PhanthomJay]

Your calc for the normal stesses at point A looks very good. However, for the shear stress at that point, you must also add the contribution from the 800 pound planar shear force to the torsional shear stress. The shear stress from the 800 pound force is maximum at this point. Q can be calculated as the area above the neutral axis times the distance from the c.g of that area to the neutral axis. The contribution to the total shear stress however will be small in comparison to the torsional shear stress.

 

[Double A]

So your saying that the shear force does apply a shear stress at location A.

I have attached a graphic of how I have my reactions acting at point A. Looking at this I don't see how the shear force would apply a shear stress. In the equation for the shear stress by a shear force include a thickness. The only thickness that I can see is the diameter of the circle since I'll be taking half the area of the circle for my Q calculation. Carrying out the calculations would result in the following:

Q = \frac{\pi r^2}{2}*\frac{4r}{3\pi} = \frac{2r^3}{3} = \frac{2(0.75 in)^3}{3} = 0.281 in^3

So now the shear stress is:

\tau_{Shear} = \frac{(800 lbs)(0.281 in^3}{(0.249 in^4)2(0.75 in)} = 601.9 psi

So then my total shear stress at point A would be:

\tau_{Total} = \tau_{Torque} + \tau_{Shear} = 16.9 ksi + 601.9 psi = 17.5 ksi

 

[PhanthomJay]

So your saying that the shear force does apply a shear stress at location A.

I have attached a graphic of how I have my reactions acting at point A. Looking at this I don't see how the shear force would apply a shear stress. In the equation for the shear stress by a shear force include a thickness. The only thickness that I can see is the diameter of the circle since I'll be taking half the area of the circle for my Q calculation. Carrying out the calculations would result in the following:

Q = \frac{\pi r^2}{2}*\frac{4r}{3\pi} = \frac{2r^3}{3} = \frac{2(0.75 in)^3}{3} = 0.281 in^3

So now the shear stress is:

\tau_{Shear} = \frac{(800 lbs)(0.281 in^3}{(0.249 in^4)2(0.75 in)} = 601.9 psi

So then my total shear stress at point A would be:

\tau_{Total} = \tau_{Torque} + \tau_{Shear} = 16.9 ksi + 601.9 psi = 17.5 ksi

That's correct. When calculating the vertical shear stress at a given point on the section, use the horizontal thickness across the section through that point, which is, in this case, the diameter. As a quick check, you can calculate the average vertical shear stress across the section , which is simply V/A = 452 psi, always less than the max shear stress which generally for a symmetrical section occurs at the neutral axis.

 

[Double A]

Thanks for the help. I think I now see how it all comes together.